Un cours de maths qui présente la fonction carrée que vous devez savoir étudier parfaitement. C'est une fonction très simple que vous allez rencontrer très souvent.
Nous allons à présent étudier la fonction carrée. C'est très simple. Retenez-la par coeur.
Définition
Fonction carrée
La fonction carrée est la fonction f définie sur par f(x) = x².La fonction carrée est une fonction paire. Donc, symétrique par rapport à l'axe des ordonnées.
Elle est décroissante sur ]-∞ ; 0] et croissante sur [0 ; +∞[.
La courbe représentative de la fonction carrée est une parabole.
Voici sa représentation graphique :
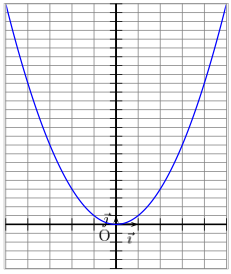
Mais pourquoi il faut connaître cette fonction par coeur ?
Cette fonction va nous aider à étudier beaucoup d'autres fonctions possédant un carré. Regardez bien le point méthode qui suit.
Point méthode : Pour étudier les variations d'une fonction f définie sur 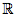 par f(x) = (x + a)² + b, vous avez deux façons de faire :
par f(x) = (x + a)² + b, vous avez deux façons de faire :
- On détermine successivement les fonctions des fonctions
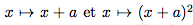 , puis on dresse le tableau de variation sachant que les variations de f(x) = (x + a)² sont les mêmes que celles de f(x) = (x + a)² + b.
, puis on dresse le tableau de variation sachant que les variations de f(x) = (x + a)² sont les mêmes que celles de f(x) = (x + a)² + b. - On monte que la courbe représentative C de la fonction f(x) = (x + a)² + b se déduit de la courbe représentative P de la fonction carrée par translation de vecteur
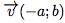 .
.
Exemple
Etudier les variations de la fonction f(x) = (x + 1)² - 2 par les deux méthodes précédentes.
- Première méthode :
La fonction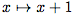 est strictement croissante et positive sur [-1 ; +∞[ et strictement croissante et négative sur ]-∞ ; -1].
est strictement croissante et positive sur [-1 ; +∞[ et strictement croissante et négative sur ]-∞ ; -1].
La fonction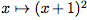 est strictement croissante sur [-1 ; +∞[ et strictement décroissante sur ]-∞ ; -1] car c'est une fonction carré.
est strictement croissante sur [-1 ; +∞[ et strictement décroissante sur ]-∞ ; -1] car c'est une fonction carré.
Donc : la fonction f est strictement croissante sur [-1 ; +∞[ et strictement décroissante sur ]-∞ ; -1]. - Seconde méthode :
Soit un point M(x ; y) appartenant à la courbe C représentative de la fonction f si et seulement si y = (x + 1)² - 2 ⇔ y + 2 = (x + 1)².
Donc le point de coordonnées (x + 1 ; y + 2) appartient à la courbe P représentative de la fonction carrée.
On passe donc de C à P par une translation de vecteur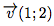 et de P à C par une translation de vecteur
et de P à C par une translation de vecteur 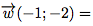
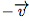 .
.
D'où la construction de C suivante :
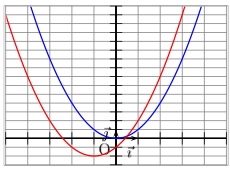
La fonction f est donc strictement croissante sur [-1 ; +∞[ et strictement décroissante sur ]-∞ ; -1].




