Aire des figures usuelles

Cours 6ème

On va maintenant voir les différentes formules d'aires des figures usuelles que vous avez apprises : carré, rectangle, triangle rectangle.

Aire d'un carré

On commence par la plus simple, l'aire d'un carré.

Définition

Aire d'un carré

Soit un carré de côté c.



L'aire de ce carré est défini par :

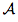= c × c = c²

Exemple

Si le carré fait 3cm de côtés, alors son aire vaut :

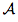= 3 × 3 = 9cm²

Vous voyez, on ne fait qu'appliquer la formule bêtement. On remplace les lettres de la formule par les chiffres donnés dans l'énoncé de l'exercice.

Aire d'un rectangle

Maintenant le rectangle.

Définition

Aire d'un rectangle

Soit un rectangle de largeur l (petit côté) et de longueur L (grand côté).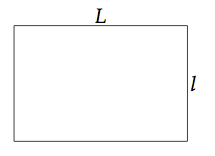



L'aire de ce rectangle est défini par :

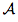= l × L

Exemple

Soit le rectangle de longueur 6cm et de largeur 4cm suivant :



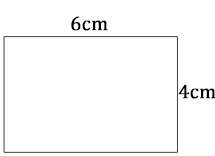
L'aire de ce rectangle est :

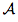= 6 × 4 = 24cm²

Aire d'un triangle rectangle

Il y a un lien entre le triangle rectangle et le rectangle justement. Essayez de le trouver...

Définition

Aire d'un rectangle

Soit un triangle rectangle de base b et de hauteur correspondante a. Ici, la hauteur correspondante n'est rien d'autre que le second côté du triangle.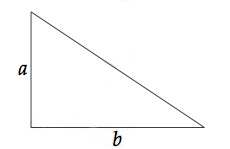



L'aire de ce triangle rectangle est défini par :

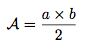
Remarque

Aire d'un disque

Je me répète : on parle d'aire d'un disque et non d'un cercle car le cercle c'est juste la bordure du disque. Ce dernier lui est remplie.

Définition

Aire d'un disque

Soit un disque de rayon r.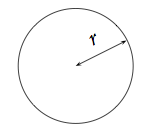




L'aire de ce disque est défini par :

= π × r × r = π × r²

Exemple

Soit le disque de rayons 3cm suivant :



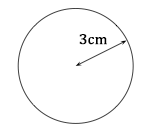
L'aire de ce disque vaut :

= π × 3 × 3 = 28,26cm²

Aire d'une figure par découpage

Parfois, on pourra vous demander de calculer l'aire d'une figure que vous ne connaissez pas. Dans ce cas là, la méthode est d'essayer de décomposer (ou recomposer) la figure en figures élémentaires dont vous connaissez les formules d'aires.

Exemple

Calculons l'aire de la figure suivante :



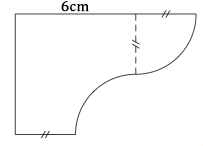
On remarque en fait que l'on peut recomposer cette figure en un carré de côté 6cm. Alors allons-y.



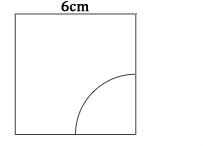
Maintenant c'est simple de calculer l'aire de la figure, car on connait parfaitement la formule de l'aire d'un carré de côté 6cm :

= 6² = 36cm²