On commence donc par ce cours sur les équations dans lequel je vous apprend à résoudre des équations de premier degré à une inconnue.
Voici quelques rappels de 4ème pour commencer.
Définition
Equation
Une équation est une égalité comportant une lettre que l'on appelle l'inconnue. Le plus souvent, cette inconnue est x.Le but est de trouver la valeur de cette inconnue pour que l'équation soit vérifiée.
Résoudre une équation, c'est donc trouver toutes les solutions de l'équation.
Propriétés
Résolution d'équations
Deux principes fondamentaux pour la résolution d'équations :- Transposition : quand on fait passer un terme d'un membre (d'un côté) à l'autre dans une équation, on change son signe.
- Multiplication et division : on peut multiplier (ou diviser) les deux membres de l'équation par un même nombre (non nul). Quand on fait passer un produit dans l'autre membre de l'équation, il devient quotient et inversement.
Exemple simple
On va résoudre l'équation suivante :
3x - 1 = -4 + 5x
On va tout d'abord rassembler tous les x d'un côté et le reste de l'autre en pensant bien à changer les signes.
3x - 5x = -4 + 1
Le 5x de droite est devenu -5x en passant à gauche et le -1 de gauche est devenu +1 en passant à droite.
On simplifie les deux côtés de l'équations maintenant que l'ont a tout bien rangé.
-2x = -3
-2x × (-1) = -3 × (-1)
2x = 3
Ce 2 du 2x va passer à droite et devenir un quotient, comme ceci :
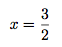
Or, la fraction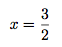 est irréductible. On a terminé le calcul.
La solution est donc :
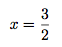
Si on remplace x par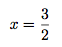, l'équation sera vérifié. Vous voulez la preuve ? Il n'y a qu'à demander !
Remplaçons tous les x de l'équation initiale par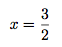 et calculons le côté gauche puis le côté droit :
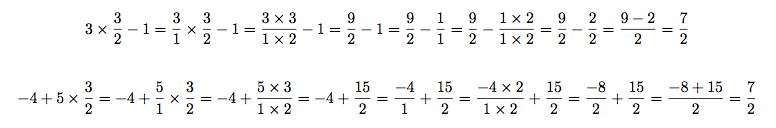
On remarque bien que les deux membres de l'équation sont égaux (les deux côtés qu'on a calculé sont égal à ). La solution est bonne. On a gagné !
On va tout d'abord rassembler tous les x d'un côté et le reste de l'autre en pensant bien à changer les signes.
Le 5x de droite est devenu -5x en passant à gauche et le -1 de gauche est devenu +1 en passant à droite.
On simplifie les deux côtés de l'équations maintenant que l'ont a tout bien rangé.
Ce 2 du 2x va passer à droite et devenir un quotient, comme ceci :
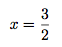
Or, la fraction
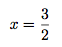est irréductible. On a terminé le calcul.
La solution est donc :
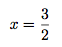
Si on remplace x par
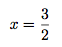, l'équation sera vérifié. Vous voulez la preuve ? Il n'y a qu'à demander !
Remplaçons tous les x de l'équation initiale par
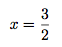et calculons le côté gauche puis le côté droit :
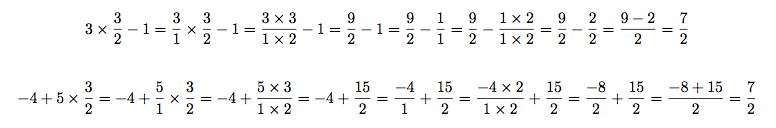
On remarque bien que les deux membres de l'équation sont égaux (les deux côtés qu'on a calculé sont égal à ). La solution est bonne. On a gagné !
Exemple plus complexe
On va résoudre l'équation suivante :
3(5x - 1) - (-x + 2) = 2
On commence par quoi ?
On commence d'abord par développer tout ça, à simplifier quoi !
3(5x - 1) - (-x + 2) = 2
15x - 3 + x - 2 = 2
16x - 5 = 2
On range tout ça : les x d'un côté, et le reste de l'autre.
16x = 2 + 5
16x = 7
On résout et on fini.
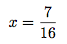
On commence par quoi ?
On commence d'abord par développer tout ça, à simplifier quoi !
On range tout ça : les x d'un côté, et le reste de l'autre.
On résout et on fini.
|
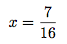
Fafa174 • il y a 2528 jours. Je crois que je commence a comprendre merci |