C'est dans ce cours que vous apprendrez ce que sont les variations d'une fonction. A travers les définitions et des exemples simples, cette notion de variations n'aura plus aucun secret pour vous.
La définition de sens de variation d'une fonction est à maîtriser absolument. Comprenez bien chaque mot de la définition qui suit.
Définition
Variations d'une fonction
Soit une fonction f définie sur un domaine D et I un intervalle de D.- f est croissante sur I si et seulement si pour tout x1, x2 ∈ I, tels que x1 ≤ x2, on a f(x1) ≤ f(x2),
- f est décroissante sur I si et seulement si pour tout x1, x2 ∈ I, tels que x1 ≤ x2, on a f(x1) ≥ f(x2),
- f est constante sur I si et seulement si il existe un k ∈
(un réel k) tel que pour tout réel x de I on f(x) = k.
Je n'ai absolument rien compris ! Pouvez-vous m'aider s'il-vous-plaît ?
Tout de suite. Je vais tout vous interpréter.
Interprétation :
- Pour une fonction croissante, plus on avance dans les x croissants, plus on avancera dans les f(x) croissants. Pour un premier x1, on aura l'image f(x1), et pour un x2 plus grand que x1, on aura un f(x2) plus grand que le f(x1). Donc la fonction monte au fur et à mesure qu'on avance dans les x, elle croît.
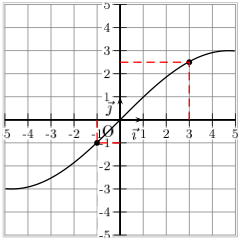
On voit bien que pour x1 = -1 ≤ x2 = 3, on a f(x1) = -1 ≤ f(x2) = 2,5. - Pour une fonction décroissante, plus on avance dans les x croissants, plus on avancera dans les f(x) décroissants. Pour un premier x1, on aura l'image f(x1), et pour un x2 plus grand que x1, on aura un f(x2) plus petit que le f(x1). Donc la fonction descend au fur et à mesure qu'on avance dans les x, elle décroît.
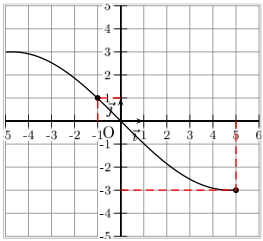
On voit bien que pour x1 = -1 ≤ x2 = 5, on a f(x1) = 1 ≥ f(x2) = -3.
Et comment on montre qu'une fonction est croissante ou décroissante ?
Il y a une méthode bien sur. Par contre, j'ai besoin de toute votre attention car il faut s'accrocher.
On prend deux éléments d'un intervalle I du domaine de définition D pour une fonction f, prenons donc a et b, tels que a < b. On doit reconstruire la fonction f pour prouver que f(a) ≤ f(b) ou que f(a) ≥ f(b).
Regardez bien l'exemple qui suit. Ce n'est pas si compliqué que ça finallement.
Exemple
On commence par prendre deux nombres positifs pour l'intervalle
+. Soit a et b positifs tels que a < b.
On pourrait faire la même chose pour l'intervalle
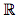- en prenant deux nombres négatifs.
On a une inégalité, on part de là pour récupérer la fonction f à gauche et à droite de l'inégalité. C'est parti !
On sait donc que a < b.
Par conséquent,
On a récupérer le premier terme de la fonction.
On peut ajouter a à gauche et b à droite car encore une fois a < b :
Ajoutons 3 à l'inégalité entière :
On a donc ici : f(a) < f(b)
C'est la définition d'une fonction croissante. La fonction f est donc croissante sur
+.
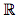Quelques exercices sur Variations d'une fonction :