1 - Définitions des triangles isométriques
On va parler ici de triangles isométriques. Les deux mots sont au pluriel. Cela vous donne déjà un indice quand à la définition que je vais vous donner.
Mais d'abord, dans triangles isométriques, on a le mot "isométrique" qui vient du mot "isométrie". Je vais vous définir cela.
Définition
Isométrie
Une isométrie est une transformation qui conserve les distances.Exemple
Vous devez avoir maintenant une idée de ce que sont deux triangles isométriques. Non, Toujours pas ?
Définition
Triangles isométriques
Deux triangles sont isométriques si l'un est l'image de l'autre par une ou plusieurs isométries successives.En fait, deux triangles isométriques sont deux triangles qui ont les côtés égaux. Se sont deux triangles parfaitement égaux, qui ont simplement était retourné, ou inverser, etc.
Exemple
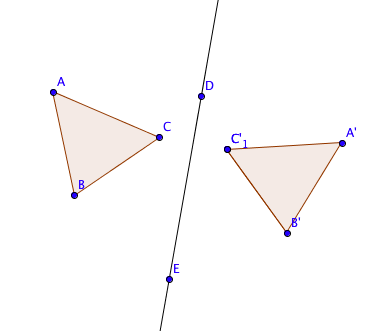
2 - Propriétés des triangles isométriques
Après la définition, vous vous doutez bien que ces triangles ont des belles propriétés. Eh bien, allons-y.
Propriétés
Propriétés des triangles isométriques
Voici les propriétés pour montrer que deux triangles sont isométriques.- Si deux triangles ont leurs trois côtés égaux, alors ils sont isométriques.
- Si deux triangles ont un angle égal compris entre deux côtés respectivement égaux, alors ils sont isométriques.
- Si deux triangles ont un côté égal et deux angles égaux, alors ils sont isométriques.
Résumons. Pour démontrer que deux triangles sont isométriques il faut, au choix :
- Trois côtés égaux,
- Un angles et les deux côtés égaux,
- Un côté et deux angle égaux.
Et pour montrer tout cela, vous avez la panoplie de propriétés et de théorèmes que je vous ai récapitulé au chapitre précédent.
Exemple
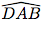 et on a DA = AF.
et on a DA = AF.
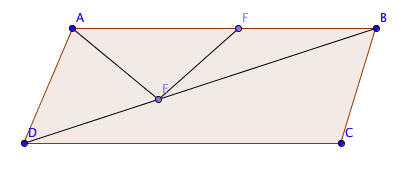
Montrons que les triangles ADF et FDE sont isométriques.
On sait que la droite (AE) est bissectrice de l'angle
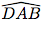 . Donc, les angles
. Donc, les angles 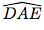 et
et 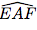 sont égaux.
sont égaux.
De plus, d'après l'énoncé, les côtés [DA] et [AF] sont égaux.
Les triangles DAE et EAF ont un côté en commun, [AE].
On a donc deux côtés égaux et un angle égaux.
On peut donc en conclure que les triangles ADE et AFE sont isométriques.
Voici un exemple un peu plus compliqué.
Exemple
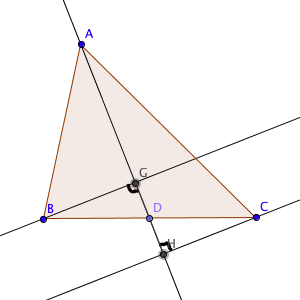
On considère un triangle ABC. Le point D est le milieu du côté [BC].
Les droites (AD) et (BG) sont perpendiculaire.
Les droites (AD) et (CH) sont perpendiculaire.
Montrer que les triangles BDG et DCH sont isométriques.
D'après l'énoncé, le point D est le milieu du segment [BC]. Donc on a : BD = DC.
De plus, les triangles BDG et DCH sont rectangles, ils ont donc un angle égaux, égal à 90°.
Ensuite, les angles
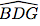 et
et 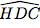 , étant opposés par leur sommet, sont égaux :
, étant opposés par leur sommet, sont égaux : 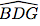 =
= 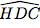 .
.
On a gagné. Je rajoute juste que dans un triangle, la somme des angles étant égale à 180°, on a en fait les trois angles des deux triangles égaux.
Trois angles et un côté égaux, on peut conclure que les triangles BDG et DCH sont isométriques.



