La fonction logarithme népérien ne "mange" que du positif. Qu'es-ce que cela veut dire ? La réponse dans ce cours sur les propriétés de la fonction logarithme.
La fonction logarithme népérien pourrait aussi se définir ainsi : c'est la fonction vérifiant :
C'est la propriété fondamentale de cette fonction. Voici les autres.
Propriétés
Propriétés de la fonction logarithme
Voici un grand nombre de propriétés sur cette fonction logarithme.- ln(1) = 0 et ln(e) = 1.
- ln x est négatif sur ]0; 1] et positif sur [1; +∞[.
- Pour tout x, y ∈
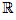 ,
,
ln x = ln y ⇔ x = y
ln x > ln y ⇔ x > y - La fonction logarithme est continue, donc dérivable, et strictement croissante sur ]0; +∞[.
- Pour tout x > 0,
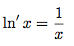
- Si u est une fonction dérivable et strictement positive sur I, alors :
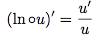
- Pour tout x, y > 0,
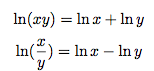
- Pour tout a réel strictement positif et tout nombre rationnel r :
ln ar = r ln a
Ces propriétés sont primordiales. Vous devez absolument les connaître sur le bout des doigts.
Je veux juste insister sur une chose en particulier.
Retenez ceci : la fonction logarithme népérien ne "mange" que du positif. Qu'es-ce que cela veut dire ?
En fait, le x du ln x doit toujours être strictement positif. Le résultat peut lui par contre être négatif.





