C'est dans ce cours sur le comportement asymptotique des fonctions, que je vais vous définir les notions d'asymptotes. Il en existe trois : asymptote verticale, horizontale et oblique.
Qu'es-ce qu'une asymptote ?
Quand es-ce que l'on rencontre une asymptote ?
Je vais vous expliquer tout cela. Sachez en premier lieu, qu'il y en trois différentes :
- Asymptote horizontale,
- Asymptote verticale,
- Asymptote oblique.
1 - Asymptote horizontale
Commençons par l'horizontale.
Définition
Asymptote horizontale
Soit f une fonction telle que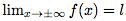
.
La droite d'équation y = l est asymptote horizontale à la courbe
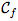en ±∞.
Remarque
Le symbole ± signifie "plus ou moins". Ce que je veux dire en l'utilisant c'est que cela revient au même en +∞ et en -∞.
Exemple
La fonction inverse admet une asymptote horizontale d'équation y = 0 en ±∞ car :
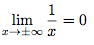
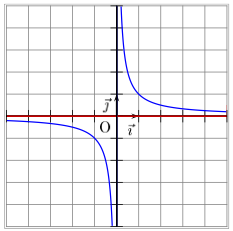
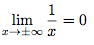
2 - Asymptote verticale
Puis la verticale.
Définition
Asymptote verticale
Soit f une fonction telle que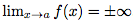
.
La droite d'équation x = a est asymptote verticale à la courbe
.
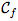Remarque
On a une asymptote verticale lorsque la fonction admet une (ou plusieurs) valeurs interdite.
Exemple
La fonction f définie par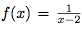 
a pour valeur interdite 2. Donc cette fonction admet une asymptote verticale d'équation x = 2,
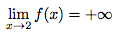
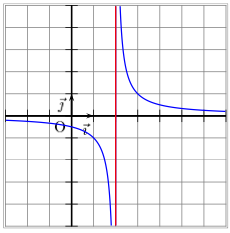
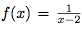a pour valeur interdite 2. Donc cette fonction admet une asymptote verticale d'équation x = 2,
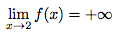
3 - Asymptote oblique
Enfin, un tout petit peu plus difficile (vraiment tout petit), l'asymptote oblique.
Définition
Asymptote oblique
La droite D d'équation y = ax + b est asymptote oblique en ±∞ à la courbe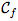 d'équation y = f(x) lorsque :
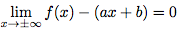
Exemple
La fonction f définie par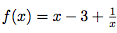 
admet une asymptote oblique d'équation y = x - 3.
En effet :
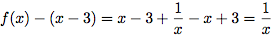
Or,
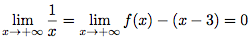
On a donc le résultat voulu.
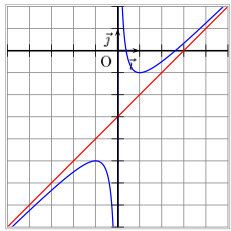
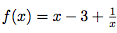admet une asymptote oblique d'équation y = x - 3.
En effet :
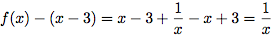
Or,
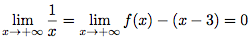
On a donc le résultat voulu.