Un cours de maths sur les limites de fonctions dans lequel je vous donne les définition des limites en l'infini ou en un point, les opérations sur les limites, la limite d'une fonction composée et même la proprité d'une fonction rationnelle polynomiale au voisinage de l'infini.
Après avoir étudié les limites de suites numériques, nous passons désormais aux limites de fonction. C'est pareil sauf que cette fois ci, la variable d'une fonction peut tendre aussi bien vers +∞ que vers -∞, autrement dit, le x peut prendre des valeurs négatives tandis que le n des suites était un entier naturel.
1 - Limite finie en l'infini
Commençons par la limite finie en +∞ et -∞.
Définition
Limite finie en l'infini
Soit f une fonction et l un réel.- La fonction f a pour limite l ∈
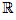 en +∞ si tout intervalle ouvert contenant l contient toutes les valeurs de f(x) pour x suffisamment grand.
en +∞ si tout intervalle ouvert contenant l contient toutes les valeurs de f(x) pour x suffisamment grand.
On note :
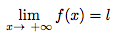
- La fonction f a pour limite l ∈
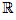 en -∞ si tout intervalle ouvert contenant l contient toutes les valeurs de f(x) pour x suffisamment petit.
en -∞ si tout intervalle ouvert contenant l contient toutes les valeurs de f(x) pour x suffisamment petit.
On note :
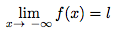
C'est presque la même définition que pour les suites.
Je vais vous expliquer ça avec des mots moins savants.
Lorsque l'on fait tendre x vers l'infini (soit vers un nombre très grand), la fonction elle va tendre vers un réel. Plus le x sera grand, plus le f(x) se rapprochera de ce réel noté l qui est la limite de la fonction.
C'est pareil pour la limite finie en -∞. Lorsque l'on fait tendre x vers -∞ (soit vers un nombre très petit), la fonction elle va tendre vers un réel. Plus le x sera petit, plus le f(x) se rapprochera de ce réel noté l qui est la limite de la fonction.
Vous avez compris ? Un petit exemple pour illustrer tout cela.
Exemple
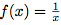 tend vers le réel 0 lorsque x tend vers l'infini. Cela veut dire que plus le x est grand, plus le f(x) sera petit et se rapprochera de la valeur 0.
tend vers le réel 0 lorsque x tend vers l'infini. Cela veut dire que plus le x est grand, plus le f(x) sera petit et se rapprochera de la valeur 0.
On note cela ainsi :
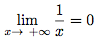
2 - Limite infinie en a
Parfois, la limite en un point est infinie.
Définitions
Limite infinie en un point
Soit f une fonction définie sur un intervalle I contenant l'intervalle ]a ; a + ε[ ou ]a - ε ; a[, avec a un réel et ε > 0.On note :
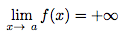
On note :
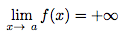
C'est juste l'inverse de la première définition. Cette fois ci, ce n'est plus le x qui grandit mais le f(x).
Lorsque l'on fait tendre x vers a, la fonction elle va tendre vers +∞. Plus le x se rapprochera de la valeur de a, plus le f(x) sera grand et tendra donc vers +∞.
Et pour l'autre : lorsque l'on fait tendre x vers a, la fonction elle va tendre vers -∞. Plus le x se rapprochera de la valeur de a, plus le f(x) sera petit et tendra donc vers -∞.
Exemple
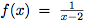 tend vers le réel l'infini lorsque x tend vers la valeur interdite de la fonction, c'est-à-dire 2. Cela veut dire que plus le x se rapproche de la valeur interdite 2, plus le f(x) sera grand.
tend vers le réel l'infini lorsque x tend vers la valeur interdite de la fonction, c'est-à-dire 2. Cela veut dire que plus le x se rapproche de la valeur interdite 2, plus le f(x) sera grand.
On note cela ainsi :
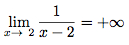
3 - Limites de fonctions de référence
Les limites que je vais vous présenter dans cette section sont usuelles. Vous devez les connaître.
Définitions
Limites de fonctions de référence
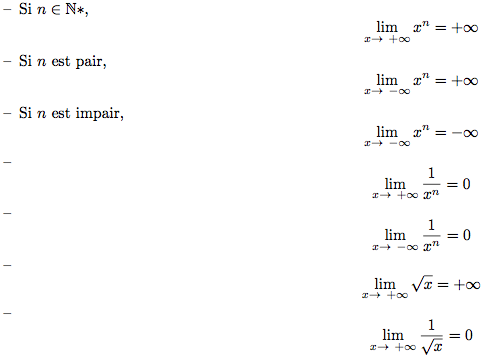
4 - Opérations sur les limites
Il nous ait déjà arrivé de faire des opérations sur les dérivées par exemple. La dérivée d'une somme est la somme des dérivées. C'est ce que nous allons faire ici mais avec des limites.
Dans cette section, a désigne soit un nombre réel, soit +∞, soit -∞ et L et L' sont des réels.
Les exemples sont en faire de section.
Propriétés

Remarque
Propriétés

Propriétés

Propriétés
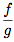 , il suffit de déterminer la limite de
, il suffit de déterminer la limite de 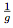 puis de déterminer la limite du produit de f par
puis de déterminer la limite du produit de f par 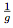 .
.
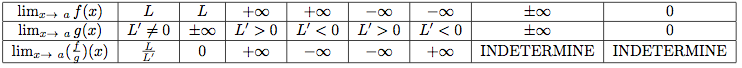
5 - Fonction rationnelle polynomiale au voisinage de l'infini
Voyons maintenant une propriété intéressante et très pratique lorsque l'on manipule des polynômes.
Propriétés
Fonction rationnelle polynomiale au voisinage de l'infini
Soit P un polynôme.- La limite de ce polynôme P en +∞ ou -∞ est égale à la limite de son terme de plus haut degré.
- La limite d'une fonction rationnelle dont le numérateur et le dénominateur sont des fonction polynômes en +∞ ou -∞ est égale à la limite du quotient des termes de plus haut degré.
Remarque importante
Exemple 1
Sa limite en +∞ est celle de son terme de plus haut degré, c'est-à-dire c'est la limite de -x5 et :
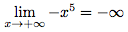
Donc, la limite de P en +∞ est -∞.
Exemple 2
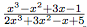 .
.
Facile. On prend les termes de plus haut degré du haut et du bas :
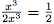 .
.
Donc :
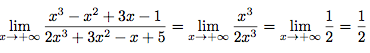
Exemple 3
Or,
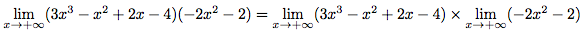
Calculons donc séparément les deux limites puis nous effectuerons leur produit.
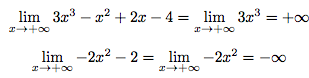
Le produit de +∞ et de -∞ est -∞.
Conclusion :
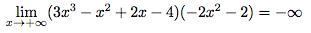
6 - Limite d'une fonction composée
Je vous redéfini la nouvelle notion de composition de fonctions.
Définition
Fonction composée
Soient f une fonction définie sur I et g(x) une fonction définie sur f(I).La fonction
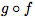 (on dit "g rond f")est la fonction définie aussi sur le domaine I par :
(on dit "g rond f")est la fonction définie aussi sur le domaine I par :
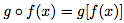
En fait, on remplace la variable de la fonction g par la fonction f.
Exemple
Si on veut
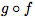 :
:
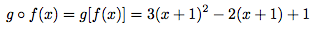
Vous avez saisie l'idée ?
Je vous laisse terminer le calcul.
Théorème
Limites des fonctions composées
Soient f une fonction définie sur I, g une fonction définie sur f(I), a un élément de I (borne comprise), L et L' deux réels ou ±∞.Si :
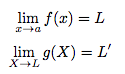
Alors :
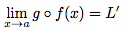
On a une première fonction f qui tend vers L lorsque sa variable x tend vers a.
Puis une seconde fonction g qui tend vers L' lorsque sa variable X tend vers L, la limite de la première fonction f.
Alors, la composée de ces deux fonction tend vers L', limite de la seconde fonction g.
C'est quelque chose d'important. C'est pourquoi je vous donne quatre exemples différents, de difficulté progressive.
Exemple 1
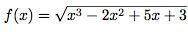 .
.
C'est la fonction g(x) = x³ - 2x² + 5x + 3 composée avec la fonction racine
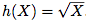 .
.
Calculons la limite de g.
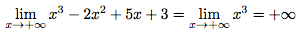
Calculons aussi la limite de h quand x tend vers la limite de g soit +∞.
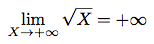
C'est facile en fait. On fait tendre l'intérieur de la racine vers l'infini. Le résultat est l'infini. Puis on regarde la limite de la racine de l'infini. Ce qui nous donne ...
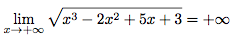
Exemple 2
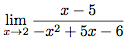
On bien que 2 est la valeur interdite de cette fraction car : -2² + 5 × 2 - 6 = 0.
On a aussi la valeur 3 comme valeur interdite mais ne nous en préoccupons pas ici, on cherche la limite en 2, pas en 3.
Nous allons devoir étudier cette limite au voisinage de 2, c'est-à-dire autour de 2. On l'étudiera en
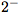 (très proche de 2 mais toujours inférieur) et en
(très proche de 2 mais toujours inférieur) et en 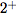 (très proche de 2 mais toujours supérieur).
(très proche de 2 mais toujours supérieur).
Nous allons donc avoir besoin du signe de la quantité -x² + 5x - 6 pour un x tendant vers
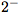 et pour un x tendant vers
et pour un x tendant vers 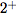 . Dressons-le.
. Dressons-le.

On voit bien donc que le polynôme -x² + 5x - 6 est négatif avant 2 et positif après. Autrement dit, en
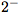 , le polynôme -x² + 5x - 6 est négatif et en
, le polynôme -x² + 5x - 6 est négatif et en 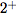 il est positif. On a ce qu'on voulait !
il est positif. On a ce qu'on voulait !
Calculons maintenant les limites :
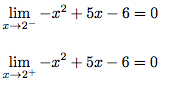
On va faire le quotient de ce polynôme.
Or, en
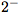 , le polynôme -x² + 5x - 6 est négatif, donc son quotient va tendre vers -∞ et en
, le polynôme -x² + 5x - 6 est négatif, donc son quotient va tendre vers -∞ et en 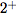 il est positif, son quotient va tendre vers +∞.
il est positif, son quotient va tendre vers +∞.
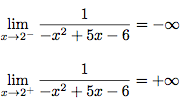
N'oublions pas la limite du numérateur.
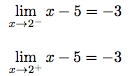
En fait, vu que 2 n'est pas une valeur interdite pour le numérateur, on a :
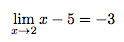
Cette limite est négative. Quand on fait le quotient des deux limites, on trouvera donc :
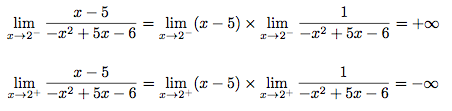
Fiou ! On a terminé. Vous voyez bien que la limites diffère en fonction de la position de x : en
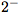 elle vaut +∞ et en
elle vaut +∞ et en 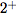 elle vaut -∞.
elle vaut -∞.
7 - Théorèmes de comparaison
Comme pour les suites, il existe des théorèmes de comparaison qui vont nous aider à déterminer la limite d'une fonction.
Cette partie est très encore une fois importante.
Dans les théorèmes que je vais vous énoncer, il y a beaucoup de conditions pré-requises. Si une d'entre elles manquent, le théorème ne peut être appliqué.
a - Théorème des gendarmes
Vous connaissez maintenant le principe.
Théorème
Théorème des gendarmes
Soient f, g et h trois fonctions telles que :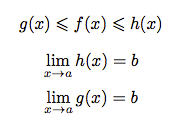
Alors, on a :
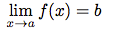
Exemple
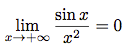
En effet, on sait que pour tout x ≠ 0, -1 ≤ sin x ≤ 1.
On divise tout par x².
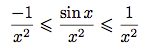
Or,
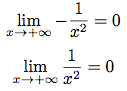
Donc, d'après le théorème des gendarmes :
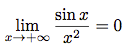
b - Comparaison au voisinage de l'infini
Deux théorèmes très pratiques basés sur la majoration et la minoration.
Théorème
Théorème de minoration
Soient b un réel, f et g deux fonctions.Si, pour tout x ∈ ]b, +&infin[,
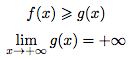
Alors :
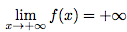
Théorème
Théorème de majoration
Soient b un réel, f et g deux fonctions.Si, pour tout x ∈ ]b, +∞[,
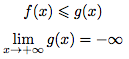
Alors :
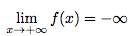
Si f est majorée par une fonction g, c'est-à-dire que f(x) ≤ g(x) et si la limite de la fonction g est -∞, alors la limite de f est plus petite que la limite de g, et plus petit que -∞ c'est forcément toujours -∞.
Pareil pour la minoration.
Exemple
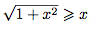 .
.
Or,
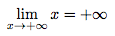
On en déduit, d'après le théorème de minoration, que :