Du deuxième étage du collège, j'aperçois dans le chantier situé en face, une grue.
Le bâtiment se trouve exactement à 19,8 mètres du pied de la grue. Placé à 8 mètres au-dessus du sol, j'ai déterminé l'angle sous lequel je voyais la grue. Cet angle BÔA est égal à 61°.
Voici une figure représentative.
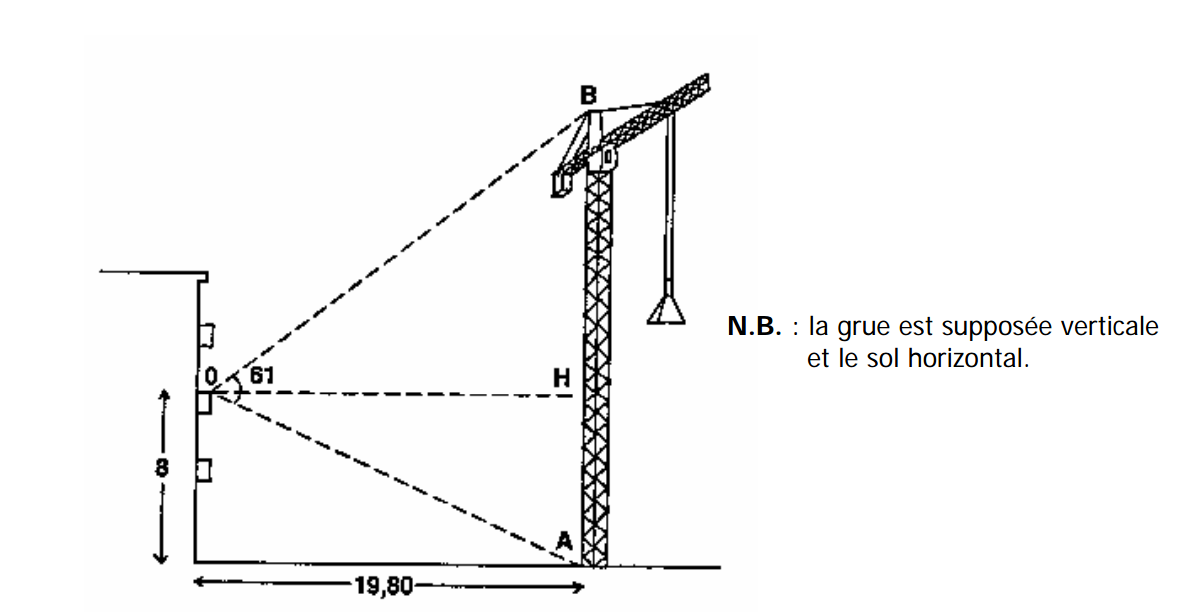
Le bâtiment se trouve exactement à 19,8 mètres du pied de la grue. Placé à 8 mètres au-dessus du sol, j'ai déterminé l'angle sous lequel je voyais la grue. Cet angle BÔA est égal à 61°.
Voici une figure représentative.

-
En appelant H le point de [BA] tel que (OH) et (AB) soient perpendiculaires, et en constatant que HA = 8 m, calculer la mesure de l'angle HÔA arrondie au degré près.
On considère le triangle OHA, rectangle en H.
On a la formule trigonométrique suivante :
tan(HOA) = AH/OH
Application numérique :
tan(HOA) = 8/19,8
En utilisant la calculatrice :
HOA ≈ 22° -
Calculer HB au cm près.
On considère le triangle OHB, rectangle en H.
On a la formule trigonométrique suivante :
tan(HOB) = HB/OH
Or, on connait la longueur OH = m. Mais que vaut l'angle HOB ?
HOB = BOA - HOA = 61° - 22° = 39°
Voici donc l'application numérique de la formule trigonométrique appliquée :
tan(39°) = HB/19,8
<=> HB = 19,8 × tan(39°) ≈ 16,03m -
En déduire la hauteur de la grue au cm près.
On peut donc en conclure la hauteur de la grue :
AB = HA + HB = 8 + 16,03 = 24,03m




