Bien évidemment, comme nous sommes dans le chapitre sur les intégrales, cet exercice aura un rapport avec l'intégration.
Pour tout x > 0 et pour tout t ∈ [0; x], on a :
Donc :
| 1 | ≤ | 1 | ≤ 1 |
|---|---|---|---|
| x + 1 | 1 + t |
Un petit coup d'intégrale sur [0; x] et le tout est joué.
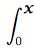 |
1 | dt ≤ 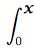 |
1 | dt ≤ 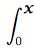 1dt 1dt |
|---|---|---|---|---|
| x + 1 | 1 + t |
Ce qui donne :
| x | ≤ ln(x + 1) ≤ x |
|---|---|
| x + 1 |