Un autre exercice sur les intégrales et les suites numériques qui, cette fois-ci, est tiré du Bac. Il est long certes, mais c'est un bon entraînement pour réussir sont Bac de maths S.
On considère la suite un définie par :
Le but de cet exercice est de déterminer la limite de la suite un.
-
- Soit la fonction définie sur [0; 2] par
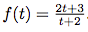 .
. - Etudier les variations de f sur [0; 2].
- En déduire que, pour tout réel t dans [0; 2],
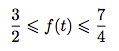 .
. - Montrer que, pour tout réel t dans [0; 2], on a :
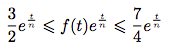 .
. - Par intégration, en déduire que :
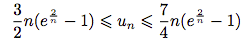 .
. - Montrer que, si un possède une limite l, alors :
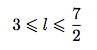 .
.
- Soit la fonction définie sur [0; 2] par
-
- Vérifier que, pour tout t ∈ [0; 2], on a :
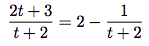 .
. - En déduire l'intégrale suivante :
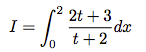 .
. - Montrer que pour tout t dans [0; 2], on a :
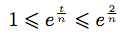 .
. - En déduire que
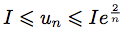 .
. - Montrer que un converge et déterminer sa limite l.
- Vérifier que, pour tout t ∈ [0; 2], on a :
Voir la correction
Révisez le cours pour mieux comprendre cet exercice Intégrale et suite numérique - Exercice tiré du Baccalauréat :