Et maintenant, on étudie les fonctions affines dans ce cours de 3ème. Image, antécédent, coefficient directeurs, ordonnée à l'origine,représentation graphique, tout y est.
Maintenant la cousine !
Définition
Fonction affine
Une fonction affine est une fonction de la forme :Avec a et b deux valeurs numériques fixées.
On procéde de la même façon que pour les fonction linéaires, avec un exemple complet.
Exemple
Soit la fonction f(x) = 2x + 1.
Calcul de l'image :
Ccomme précédemment, on remplace x par les valeurs que l'on veut.
f(-2) = -3
f(-1) = -1
f(0) = 1
f(1) = 3
f(2) = 5
L'image de (-2) par f est (-3), que l'image de 0 par f est 1, etc.
Calcul de l'antécédent :
Cherchons par exemple l'antécédent de 2 par la fonction f.
On cherche donc x, tel que f(x) = 2.
On résout :
2x + 1 = 2
2x = 1
Et on trouve :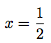
Donc, l'antécédent de 2 par f est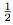 .
.
Représentation graphique : à l'aide des images que l'on vient de calculées, on construit le tableau suivant :
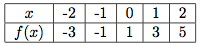
On dit que l'on trace la droite d'équation : y = 2x + 1.
Cette droite passe par le point de coordonnées (0 ; f(0)).
f(0) se lit directement sur la fonction : f(0)=1. Nous reviendrons à la fin de ce cours sur cette notion.
Représentation graphique de la fonction f :
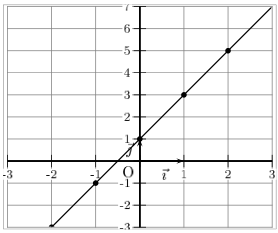
Calcul de l'image :
Ccomme précédemment, on remplace x par les valeurs que l'on veut.
f(-2) = -3
f(-1) = -1
f(0) = 1
f(1) = 3
f(2) = 5
L'image de (-2) par f est (-3), que l'image de 0 par f est 1, etc.
Calcul de l'antécédent :
Cherchons par exemple l'antécédent de 2 par la fonction f.
On cherche donc x, tel que f(x) = 2.
On résout :
2x = 1
Et on trouve :
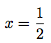
Donc, l'antécédent de 2 par f est
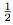 .
.
Représentation graphique : à l'aide des images que l'on vient de calculées, on construit le tableau suivant :

On dit que l'on trace la droite d'équation : y = 2x + 1.
Cette droite passe par le point de coordonnées (0 ; f(0)).
f(0) se lit directement sur la fonction : f(0)=1. Nous reviendrons à la fin de ce cours sur cette notion.
Représentation graphique de la fonction f :

Remarque/Exemple
Si on vous demande de retrouver une fonction affine f tel que f(1) = 0 et f(2) = 4 :
On revient, encore et toujours, à la définition. On sait qu'une fonction affine est de la forme f(x) = ax + b, on cherche le a et le b.
Mais on ne sait pas résoudre une équation avec deux inconnues ?!
Non, c'est vrai. En tous les cas, il y aurait une infinité de solutions. Mais qui vous parle d'une équation ? C'est un système que l'on va résoudre cette fois.
Or, f (1) = 0 et f (2) = 4.
Donc :
a × 1 + b = 0
a × 2 + b = 4
On résout donc le système suivant :
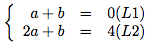
On va faire (L1) - (L2).
-a = -4
a = 4
Ont rouge ensuite b :
a + b = 0
a = -b
b = -4
Donc, le couple de solution de ce système est (4 ; -4).
Et donc la fonction recherchée est :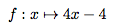
Je vous laisse vérifier.
On revient, encore et toujours, à la définition. On sait qu'une fonction affine est de la forme f(x) = ax + b, on cherche le a et le b.
Mais on ne sait pas résoudre une équation avec deux inconnues ?!
Non, c'est vrai. En tous les cas, il y aurait une infinité de solutions. Mais qui vous parle d'une équation ? C'est un système que l'on va résoudre cette fois.
Or, f (1) = 0 et f (2) = 4.
Donc :
a × 2 + b = 4
On résout donc le système suivant :
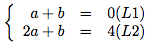
On va faire (L1) - (L2).
a = 4
Ont rouge ensuite b :
a = -b
b = -4
Donc, le couple de solution de ce système est (4 ; -4).
Et donc la fonction recherchée est :
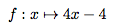
Je vous laisse vérifier.
Je vous avais dit que je reviendrai sur une notion importante. Je me suis trompé en disant qu'elle était importante. Elle est ultra importante. La voici.
Définitions
Coefficient directeur et ordonnée à l'origine
Soit une fonction affine f(x) = ax + b. Sa droite d'équation est : y = ax + b.a s'appelle le coefficient directeur de la droite et b s'appelle l'ordonnée à l'origine de la droite.
Le coefficient directement se traduit aisément sur une droite. Quand la droite avance d'un pas vers la droite, elle monte de a pas vers le haut (si a est positif) ou vers le bas (si a est négatif).
L'ordonnée à l'origine traduit le point de coordonnées (0 ; f(0)), avec f(0) = b.





