Le premier type de fonction que nous allons étudier dans ce cours est la fonction linéaire avec sa définition, sa forme et sa représentation graphique.
Je vais vous présenter la notion de fonction linéaire, elle est très simple mais doit être bien comprise pour la suite du cours quand on abordera sa cousine, la fonction affine.
Définition
Fonction linéaire
Une fonction linéaire est une fonction de la forme :Avec a une valeur numérique fixée.
Remarque
En fait, une fonction linéaire marque une relation de proportionnalité.
Exemple
La fonction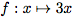 
est une fonction linéaire.
Allez, étudions une fonction linéaire avec calcul d'image, d'antécédent et représentation graphique.
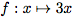est une fonction linéaire.
Allez, étudions une fonction linéaire avec calcul d'image, d'antécédent et représentation graphique.
Exemple
Soit la fonction f(x) = 5x.
Calcul de l'image :
On remplace simplement x par les valeurs que l'on veut.
f(-1) = -5
f(0) = 0
f(1) = 5
f(2) = 10
f(3) = 15
On dit que l'image de (-1) par f est (-5), que l'image de 0 par x est 0, etc.
On pourrait continuer ainsi, mais nous n'avons pas que cela à faire !
Calcul de l'antécédent :
Cherchons par exemple l'antécédent de 3 par la fonction x.
On cherche donc x (oui, x est l'antécédent), tel que f(x) = 3.
Et comment on fait ?
Simple équation. On résout ceci : 5x = 3.
Et on trouve :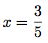
Donc, l'antécédent de 3 par f est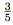
.
Représentation graphique : à l'aide des images calculées tout-à-l'heure, on construit le tableau suivant :
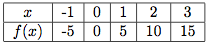
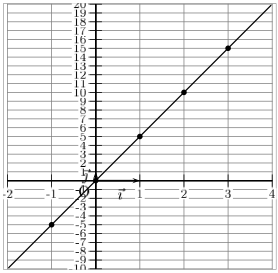
On trace enfin la fonction f, et puis voilà.
Calcul de l'image :
On remplace simplement x par les valeurs que l'on veut.
f(-1) = -5
f(0) = 0
f(1) = 5
f(2) = 10
f(3) = 15
On dit que l'image de (-1) par f est (-5), que l'image de 0 par x est 0, etc.
On pourrait continuer ainsi, mais nous n'avons pas que cela à faire !
Calcul de l'antécédent :
Cherchons par exemple l'antécédent de 3 par la fonction x.
On cherche donc x (oui, x est l'antécédent), tel que f(x) = 3.
Et comment on fait ?
Simple équation. On résout ceci : 5x = 3.
Et on trouve :
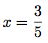
Donc, l'antécédent de 3 par f est
.
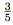Représentation graphique : à l'aide des images calculées tout-à-l'heure, on construit le tableau suivant :
On trace enfin la fonction f, et puis voilà.
Remarque/Exemple
Si on vous demande de retrouver une fonction linéaire g (Eh oui, toutes les fonctions ne s'appellent pas f, on peut les appeler comme on veut) tel que g(2) = 6, voilà comment procéder :
On revient à la définition. On sait qu'une fonction linéaire est de la forme g(x) = ax, on cherche le a.
Or, g(2) = 6.
Donc : g(2) = 2 × a = 6
On résout et on trouve : a = 3.
Et en effet, l'antécédent de 2 par la fonction g(x) = 3x est bien 6.
On revient à la définition. On sait qu'une fonction linéaire est de la forme g(x) = ax, on cherche le a.
Or, g(2) = 6.
Donc : g(2) = 2 × a = 6
On résout et on trouve : a = 3.
Et en effet, l'antécédent de 2 par la fonction g(x) = 3x est bien 6.