Une méthode simple mais sûre, pour résoudre n'importe quel système de deux équations à deux inconnues. Etape par étape, je vous montre comment résoudre un exemple de système d'équations.
Ce cours méthode va vous apprendre à résoudre des systèmes de deux équations à deux inconnues. Prenons un exemple dans lequel il va falloir résoudre le système suivant :
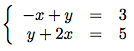
Réordonner les colonnes du système
Avant de pouvoir résoudre le système, il va nous falloir passer par plusieurs étapes simples. Comme celle-ci. Nous allons avant tout réordonné les colonnes de ce système. Le but est d'avoir une colonne avec les x et une autre avec les y.
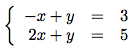
Eliminer l'une des deux inconnues
On va maintenant tenter d'éliminer l'une des deux inconnues du système (x ou y). Pour cela, nous allons dans notre exemple multiplier la première équation (entièrement, à gauche et à droite) par (-1) pour éliminer les y après addition des deux équations. On y va ? C'est parti !
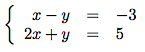
Additionner les deux équations pour trouver x
A présent, additionnons les deux équations, pour obtenir :
Résolvons cette équation simplement :
Déterminer la seconde inconnue grâce à la première
On a maintenant trouvé le x.
Utilisons ce x pour déterminer y à présent.
On le remplace dans l'équation que l'on veut pour ensuite trouvé le y. Moi j'ai choisi de le remplacer dans la première équation car c'est la plus simple.
Ce qui nous donne :
Enfin, on a trouvé la solution du système :
Et les systèmes servent notamment à résoudre des problèmes. Vous le verrez dans le prochain cours méthode.




