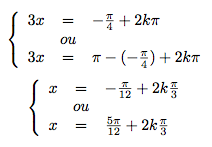Un cours sur les résolutions d'équations trigonométriques dans lequel, après vous avoir donné la méthode, je vous montre comment résoudre des équations faisant intervenir des cosinus et des sinus.
Nous allons maintenant nous servir de tout cela.
Propriétés
Résolution d'équations trigonométriques
Soit k un entier.- Résolution de cos x = a :
- Si |a| > 1, il n'y a pas de solution,
- |a| ≤ 1, alors il existe α ∈ [0,π] tel que cos α = a. L'équation devient alors cos x = cos α et on a donc :
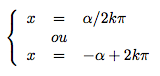
- Résolution de sin x = a :
- Si |a| > 1, il n'y a pas de solution,
- |a| ≤ 1, alors il existe α ∈ [-
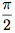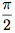,] tel que sin α = a. L'équation devient alors sin x = sin α et on a donc :
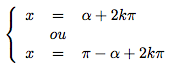
Je vais vous donner un exemple de chaque.
Exemple 1
Résoudre l'équation suivante : 2cos3x + 1 = 0.
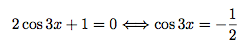
Or,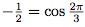
.
Donc :
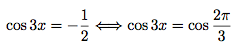
D'où :
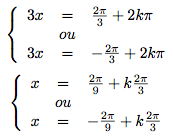
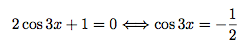
Or,
.
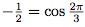Donc :
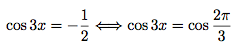
D'où :
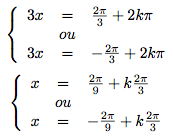
Exemple 2
Résoudre l'équation suivante : √2sin3x + 1 = 0.
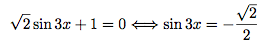
Or,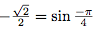
.
Donc :
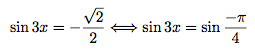
D'où :
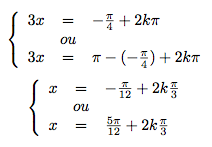
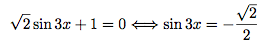
Or,
.
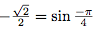Donc :
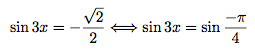
D'où :