Savez-vous ce qu'est une fonction composée ? Je vous explique tout ça dans ce cours de maths. Je vous apprendrai également à calculer la dérivée d'une fonction composée, vous risquez de tomber sur ça lors du Bac.
Nous avions déjà parlé des fonction composées.
Je vous le rappelle briévement.
Définition
Composition de fonctions
Soient f une fonction définie sur I et g(x) une fonction définie sur f(I).La fonction
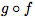(on dit "g rond f") est la fonction définie aussi sur le domaine I par :
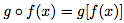
En fait, on remplace la variable de la fonction g par la fonction f.
Exemple
Soient deux fonctions f(x) = x + 1 et g(x) = 3x² - 2x + 1.
Si on veut :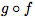
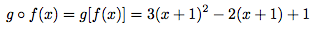
Vous avez saisi l'idée ?
Je vous laisse terminer le calcul.
Si on veut
:
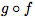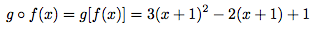
Vous avez saisi l'idée ?
Je vous laisse terminer le calcul.
Eh bien, dés à présent, vous saurez calculer la dérivée d'une fonction composée directement à l'aide de la formule suivante.
Théorème
Dérivation d'une fonction composée
Soient f une fonction définie sur I et g une fonction définie sur f(I).On a la formule suivante :
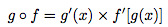
Exemple
Soit la fonction f définie par : f(x) = sin(x² + 2x + 1).
On a les fonctions h(x) = sin x et g(x) = x² + 2x + 1.
La dérivée de g est donc : g'(x) = 2x + 2.
La dérivée de h est : h'(x) = cos x.
Appliquons la formule : f'(x)= g'(x) × h'[g'(x)] = (2x + 2) cos(x² + 2x + 1).
On a les fonctions h(x) = sin x et g(x) = x² + 2x + 1.
La dérivée de g est donc : g'(x) = 2x + 2.
La dérivée de h est : h'(x) = cos x.
Appliquons la formule : f'(x)= g'(x) × h'[g'(x)] = (2x + 2) cos(x² + 2x + 1).
|
Fbaxmc • il y a 1700 jours. Faute dans le cours |
|
|
Fbaxmc • il y a 1700 jours. Faute dans le cours |