Amateur de sudoku, Hadrien s’entraîne très souvent. Il adore ce jeu.
50% des grilles de sudoku qui y sont proposées sont de niveau facile, 30% sont de niveau moyen et 20% de niveau difficile.
Hadrien sait qu’il réussit les grilles de sudoku de niveau facile dans 80% des cas, les grilles de sudoku de niveau moyen dans 50% des cas et les grilles de sudoku de niveau difficile dans 25% des cas.
Une grille de sudoku lui est proposée de façon aléatoire.
Pour cet exercice, on considèrera les événements suivants :
- F : « la grille est de niveau facile »,
- M : « la grille est de niveau moyen »,
- D : « la grille est de niveau difficile »,
- R : « Hadrien réussit la grille » et R son événement contraire.
50% des grilles de sudoku qui y sont proposées sont de niveau facile, 30% sont de niveau moyen et 20% de niveau difficile.
Hadrien sait qu’il réussit les grilles de sudoku de niveau facile dans 80% des cas, les grilles de sudoku de niveau moyen dans 50% des cas et les grilles de sudoku de niveau difficile dans 25% des cas.
Une grille de sudoku lui est proposée de façon aléatoire.
Pour cet exercice, on considèrera les événements suivants :
- F : « la grille est de niveau facile »,
- M : « la grille est de niveau moyen »,
- D : « la grille est de niveau difficile »,
- R : « Hadrien réussit la grille » et R son événement contraire.
-
Construire un arbre pondéré résumant la situation de l'énoncé.
On peut, grâce aux données de l'énoncé, construire l'arbre pondéré représentant la situation :
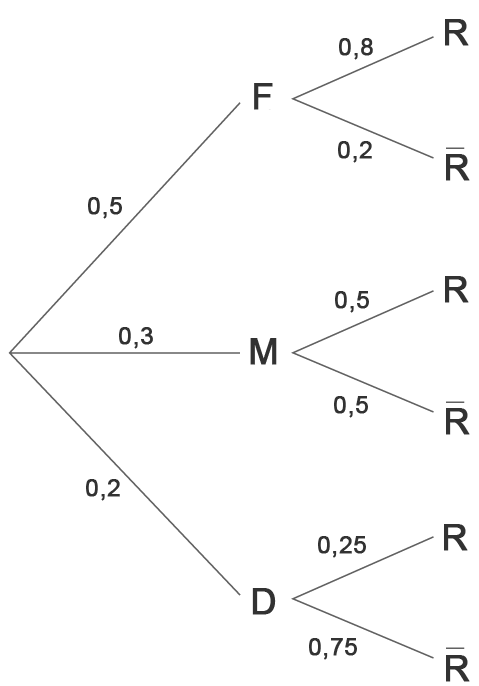
-
Calculer la probabilité que la grille proposée soit facile et que Hadrien la réussisse.
On cherche P(F ∩ R).
D'après l'arbre pondéré de la question précédente, on trouve :
P(F ∩ R) = P(F) × PF(R)
P(F ∩ R) = 0,5 × 0,8 = 0,4
La probabilité que la grille proposée soit facile et que Hadrien la réussisse est égale à 0,4. -
Calculer la probabilité que la grille proposée soit difficile et que Hadrien ne la réussisse pas.
On cherche P(D ∩ R).
D'après l'arbre pondéré de la question précédente, on trouve :
P(D ∩ R) = P(D) × PD(R)
P(D ∩ R) = 0,20 × 0,75 = 0,15
La probabilité que la grille proposée soit difficile et que Hadrien ne la réussisse pas est égale à 0,15. -
Montrer que la probabilité que Hadrien réussisse la grille proposée est égale à 0,6.
On cherche en réalité P(R).
D'après l'arbre pondéré de la question précédente, on trouve trois chemins pour arriver à R :
- P(F ∩ R) = 0,5 ×, 0,8 = 0,4
- P(M ∩ R) = 0,3 ×, 0,5 = 0,15
- P(D ∩ R) = 0,2 ×, 0,25 = 0,05
Il suffit maintenant d'additionner ces probabilités :P(R) = P(F ∩ R) + P(M ∩ R) + P(D ∩ R)
P(R) = 0,4 + 0,15 + 0,05
P(R) = 0,6
La probabilité que Hadrien réussisse la grille proposée est en effet égale à 0,6. -
Sachant que Hadrien n’a pas réussi la grille proposée, quelle est la probabilité que ce soit une grille de niveau facile ?
On cherche PR(F).
Or, si on connait son cours, on sait que :
PR(F) = P(R ∩ F) P(R)
Calculons P(R ∩ F) :
P(R ∩ F) = 0,5 ×, 0,2 = 0,1
Calculons à présent P(R) comme suit :
P(R) + P(R) = 1
P(R) = 1 - P(R)
P(W) = 1 - 0,6
P(W) = 0,4
Maintenant, on peut appliquer la première formule pour calculer PR(F).
PR(F) = 0,1 0,4
PR(F) = 0,25
Sachant que Hadrien n’a pas réussi la grille proposée, la probabilité que ce soit une grille de niveau facile est égale à 0,25. -
Hadrien a réussi la grille proposée. Son ami Jean pense que sa grille était facile.
Dans quelle mesure a-t-il raison ? Justifier.On cherche PR(F).
Or, si on connait son cours, on sait que :
PR(F) = P(R ∩ F) P(R)
On a toutes les données (grâce aux questions précédentes) pour effectuer ce calcul :
PR(F) = 0,4 0,6
PR(F) = 0,67
Sachant que Hadrien a réussi la grille proposée, la probabilité que ce soit une grille de niveau facile est égale à 0,67.
Donc, son ami Jean a 67% de chance d'avoir raison.