La fonction inverse est un peu plus complexe car c'est un quotient, elle a donc une valeur interdite. Dans ce cours, je l'étudie avec vous pour vous en donner les moindres détails.
Et maintenant, étudions la fonction inverse.
Définition
Fonction inverse
La fonction inverse est la fonction f définie sur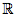 - {0} (appelé aussi
- {0} (appelé aussi 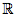 +) par
+) par 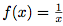 .
.
La fonction inverse est une fonction impaire. Donc, son centre de symétrie est l'origine du repère.
Elle est décroissante sur
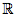 + et décroissante sur
+ et décroissante sur  -.
-.
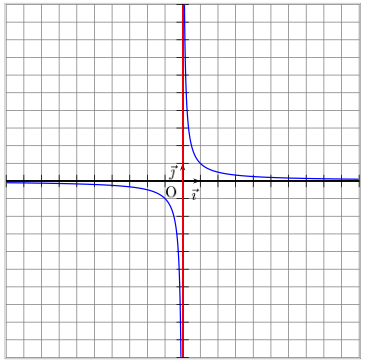
La courbe représentative de la fonction carrée est une hyperbole.
Elle possède une asymptote verticale en x = 0 et une asymptote horizontale d'équation y = 0. En effet, 0 est une valeur interdite (donc asymptote verticale), et elle ne peut pas être nulle (donc asymptote horizontale).
Voici sa représentation graphique :
Cette fonction aussi nous aide à l'étude d'autre fonctions du même type ?
Oui, regardez.
Point méthode : Pour étudier les variations d'une fonction f définie sur 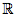 par
par 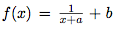 , vous avez deux façons de faire :
, vous avez deux façons de faire :
- On détermine successivement les fonctions des fonctions
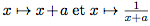 , puis on dresse le tableau de variation sachant que les variations de
, puis on dresse le tableau de variation sachant que les variations de 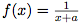 sont les mêmes que celles de
sont les mêmes que celles de 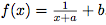 .
. - On monte que la courbe représentative C de la fonction
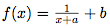 se déduit de la courbe représentative P de la fonction inverse par translation de vecteur
se déduit de la courbe représentative P de la fonction inverse par translation de vecteur 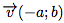 .
.
Je ne donne pas d'exemple pour cette partie là. C'est exactement de la même façon que pour la section précédente.




