On commence par un chapitre sur la parité. Vous apprendrez dans ce cours ce qu'est uen fonction paire et une fonction impaire à travers une définition et des exemples.
On distingue des fonctions paires et des fonctions impaires.
Définition
Fonction paire
Soit une fonction f définie sur un domaine D.La fonction f est paire si pour tout éléments x de D, f(-x) = f(x) (avec -x ∈ D).
Sa courbe représentative admet l'axe des ordonnées comme axe de symétrie.
Définition
Fonction impaire
Soit une fonction f définie sur un domaine D.La fonction f est impaire si pour tout éléments x de D, f(-x) = -f(x) (avec -x ∈ D).
Sa courbe représentative admet l'origine du repère comme centre de symétrie.
Attention
Si une fonction n'est pas paire, elle n'est pas forcément impaire (et inversement). Une fonction peut être ni paire ni impaire.
Exemples
Voici un exemple de chaque.
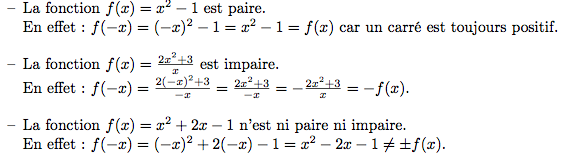
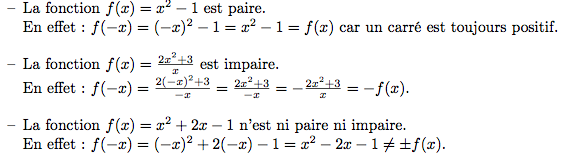
|
|
Misswissa21 • il y a 2180 jours. Bonjour. je pense que mettre les courbes paires et impaires sur un graphique peut mieux nous faire comprendre en quoi une fonction paire est symétrique par rapport à l'axe des ordonnés. Merci. Au revoir |




