Voici un cours sur les droites remarquables du triangles : médiatrice, médiane, hauteur et bissectrice. Vous devez les reconnaître et savoir les tracer.
Je vous rappelle (encore une fois) que dans un triangle, il existe des droites qui ont une signification mathématiques et qui vont nous aider à faire des calculs sur les triangles, comme par exemple calculer leur aire.
Dans cette partie sur les droites remarquables du triangle, nous allons en étudier : les hauteurs, les médiane, les médiatrices et les bissectrice.
Hauteur
On va commencer par les hauteurs d'un triangle.
Définition
Définition de la hauteur d'un triangle
La hauteur issue d'un sommet d'un triangle est la droite qui passe par ce sommet et qui est perpendiculaire au côté opposé.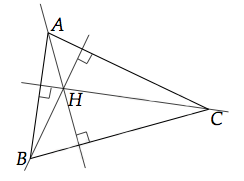
Donc, vous prenez un côté d'un triangle, vous tracer une droite perpendiculaire à ce côté et passant par le sommet opposé. Cette droite est une des hauteurs du triangle. J'ai bien dis une des hauteurs du triangle car un triangle a trois côtés, donc trois hauteurs.
Remarque
Remarque importante
Médiane
Maintenant les médianes d'un triangle.
Définition
Définition de la médiane d'un triangle
La médiane issue d'un sommet d'un triangle est la droite passant par ce sommet et par le milieu du côté opposé.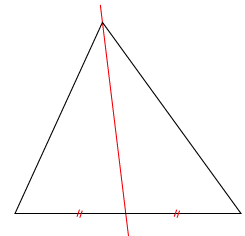
Prenez un côté d'un triangle, vous tracer une droite qui passe par le milieu de ce côté et passant par le sommet opposé. Cette droite est une des médianes du triangle. J'ai bien dis une des médianes du triangle car un triangle a trois côtés, donc trois médianes.
Remarque importante
Médiatrice
On parlera de la médiatrice d'un segment.
Définition
Définition de la médiatrice d'un triangle
La médiatrice d'un segment est la droite qui passe perpendiculairement en son milieu.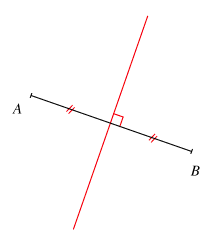
Donc, vous prenez un segment, vous tracer une droite qui passe par son milieu et qui y forme un angle droit. Cette droite est la médiatrice de ce segment.
Remarque
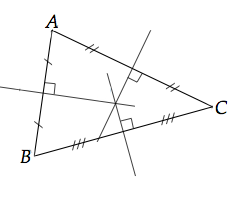
Propriété
Propriété des médiatrices
Si un point est sur la médiatrice d'un segment, il est à égale distance des extrémités de ce segment.Inversement, si un point est à égale distance des extrémités d'un segment, il appartient à la médiatrice de ce segment.
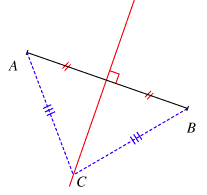
Remarque
Bissectrice
Vous rappelez-vous de ce qu'est la bissectrice d'un angle ?
Définition
Définition de la bissectrice d'un angle
La bissectrice d'un angle est la demi-droite qui sépare l'angle en deux angles de même mesure.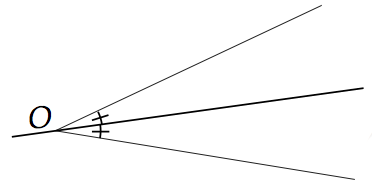
Et comment on construit la bissectrice d'un angle ?
Prenons l'angle suivant.
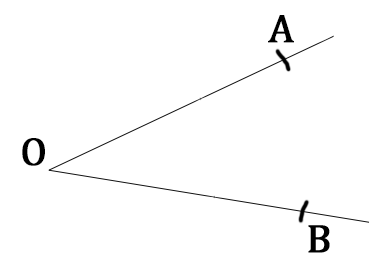
Nous allons tracer la bissectrice de cet angle AÔB.
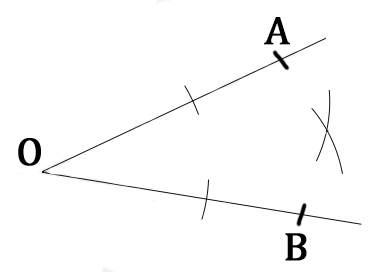
Commençons d'abord par tracer sur chacune de ces demi-droites [OA) et [OB) deux arcs de cercle centrés en O et de même rayon. En fait, vous pointez le compas sur O et vous l'ouvrez autant que vous voulez et faites deux arcs de cercle sur chacune des demi-droites.
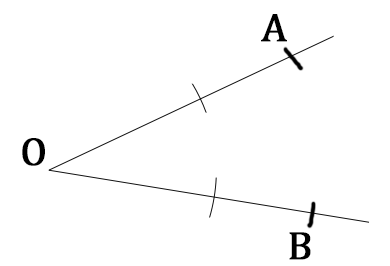
A partir de ces deux points, on trace à nouveau deux arcs de cercles de même rayon qui se coupent. Donc on pointe le compas sur le premier arc de cercle, on ouvre le compas comme on veut et on trace un arc de cercle. Pareil avec le second.
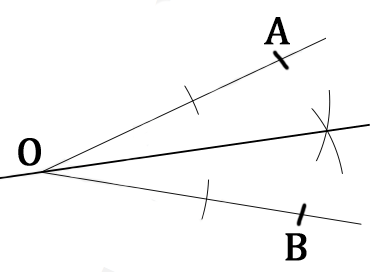
La bissectrice est obtenue en traçant la droite qui passe par ce dernier point et par le sommet O de l'angle.
Je peux donc maintenant vous donner la définition du cercle inscrit à un triangle. Evidemment, vous l'aurez compris, il y a un lien avec les bissectrices. Mais lequel ?
Définition
Cercle inscrit
Dans un triangle, les bissectrices des trois angles se coupent en un même point, qui est le centre du cercle inscrit dans le triangle. Ce cercle est tangent aux trois côtés du triangle.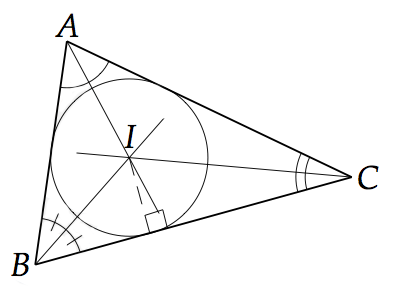
Le cercle circonscrit à un triangle c'est le cercle à l'extérieur du triangle, et le cercle inscrit à un triangle, c'est celui qui est à l'intérieur. Et comme il est à l'intérieur, son centre est forcément lui aussi, à l'intérieur du triangle.




