Ce cours sur les probabilités conditionnelle en terminale S est constitué de trois parties : conditionnement, indépendance et la formule des probabilités totales.
Dans ce cours sur les probabilités conditionnelles, nous traiterons d'abord le conditionnement, puis l'indépendance et nous finirons par la formule des probabilités totales.
Conditionnement
Je vais vous introduire cette partie sur le conditionnement avec un exemple simple, celui d'un jeu de 54 cartes décomposées comme suit : 13 ♥, 13 ♦, 13 ♣, 13 ♠ et 2 jokers.
Nous allons appliquer toutes les propriétés de probabilité vues précédemment dans cet exemple de jeu de cartes.
Définissons tout d'abord deux événements :
- L'événement A est "obtenir un As",
- L'événement B est "obtenir un coeur".
Combien y a-t-il de coeurs dans ce jeu ? 13 d'après l'énoncé. Donc, la probabilités d'avoir un coeur est de 13/54, que l'on note ainsi :
Combien y a-t-il d'As de coeurs dans ce jeu de cartes ? Un seul sur les 54 cartes. On notera donc :
Combien y a-t-il d'As dans l'ensemble des coeurs du jeu ? Un seul en effet. Un seul sur les 13 coeurs du jeu de 54 cartes. Là on croise la probabilité de A et celle de B, on calcule la probabilité de A sur un univers sui se réduit à l'ensemble des coeurs, on dit "probabilité de A sachant B" et l'on note ça :
Oh mais... Que remarque-je ? Que :
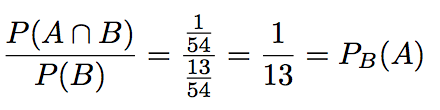
C'est la propriété des probabilités conditionnelles !
Définition
Conditionnement
Soient A et B deux événements, avec A de probabilité non nulle.On définit la probabilité de A sachant B par :
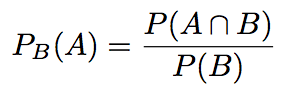
C'est une formule incontournable dans ce chapitre sur le conditionnement. Grâce à elle, vous saurez calculer la majorité des probabilités "simples" que l'on vous demandera.
Indépendance
Pour cette partie, prenons à présent un jeu de 52 cartes cette fois-ci : 13 ♥, 13 ♦, 13 ♣, 13 ♠, donc sans les jokers.
Reprenons les deux mêmes événements :
- L'événement A est "obtenir un As",
- L'événement B est "obtenir un coeur".
Que remarque-t-on ? Que :
En gros, cela veut dire que la proportion des As dans ce jeu de 52 cartes est la même que la proportion des As dans l'ensemble des coeur. On a une chance sur 13 de tomber sur un As parmi les 52 cartes et une chance sur 13 de tomber sur un As de coeur parmi les coeurs.
On dira que les événements A et B sont indépendants, soit que B n'a pas d'influence sur la réalisation de A.
De là, je vous donne la définition de l'indépendance.
Définition
Indépendance
Deux événements A et B sont indépendants si et seulement si :
Nous pouvons énoncer également le théorème suivant.
Théorème
Théorème de l'indépendance
Soient A et B deux événements de probabilités non nulles.On a alors :
Je vous l'ai prouvé dans l'exemple d'introduction, donc pas besoin d'en rajouter.
Formule des probabilités totales
Une formule pour clôturer ce cours sur les probabilités conditionnelles, celle des probabilités totales.
Avant cela, juste une petite définition d'une partition en probabilité.
Définition
Partition
Soit un ensemble E.Les événements de probabilités non nulles {E1; E2; E3; ...; En} forment une partition de E si et seulement si :
- ∀ i ∈ [|1; n|], Ei ∈ E,
- Les événements E1, E2, ..., En sont deux à deux incompatibles,
- Leur réunion est égale à l'ensemble E.
Maintenant la formule des probabilités totales peut être énoncée..
Propriété
Formule des probabilités totales
Soit (A1; A2; ...; An) une partition de Ω.Alors, pour tout événement B de Ω, on aura :
Un petit exemple pour appliquer tout ça et pour que vous compreniez l'intérêt.
Exemple
Quelle est la proportion des consommateurs de café dans l'entreprise ?
Alors... Quelle formule allons-nous appliquer ? Oui, bien sûr, la formule des probabilités totales, on vient de la voir en même temps...
Définissons les deux événements du problème :
- L'événement F est "être une femme",
- L'événement C est "boire du café".
Vous l'avez compris, on cherche P(C).
Représentons la situation pour que cela soit plus clair dans votre esprit.
Avant tout calcul, nous devons impérativement construire l'arbre pondéré.
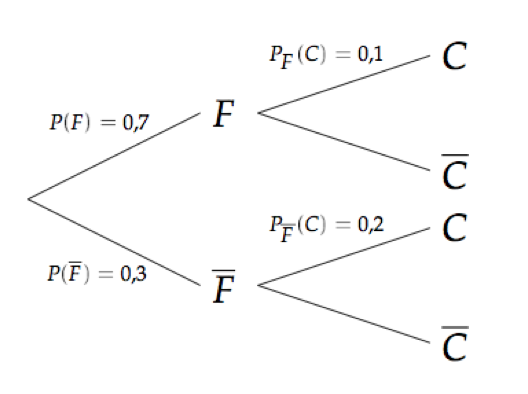
Pas de problème pour construire cet arbre, rien de plus simple avec l'énoncé explicite.
D'après cet arbre pondéré, on peut remarquer que :
Ce qui veut dire tout simplement que l'ensemble des consommateurs de café sont les femmes qui consomment du café ((C ∩ F) et les hommes qui consomment du café ((C ∩ F)).
Comme ce sont des événements incompatibles, on peut appliquer la formule des probabilités totales :
On fait l'application numérique :
Conclusion : la proportion des consommateurs de café est de 13%.
|
|
Avogadrodz • il y a 2533 jours. C est bien |
|
|
Cheikh_cheikhgueyecheikh- • il y a 3898 jours. Bien libelé |




