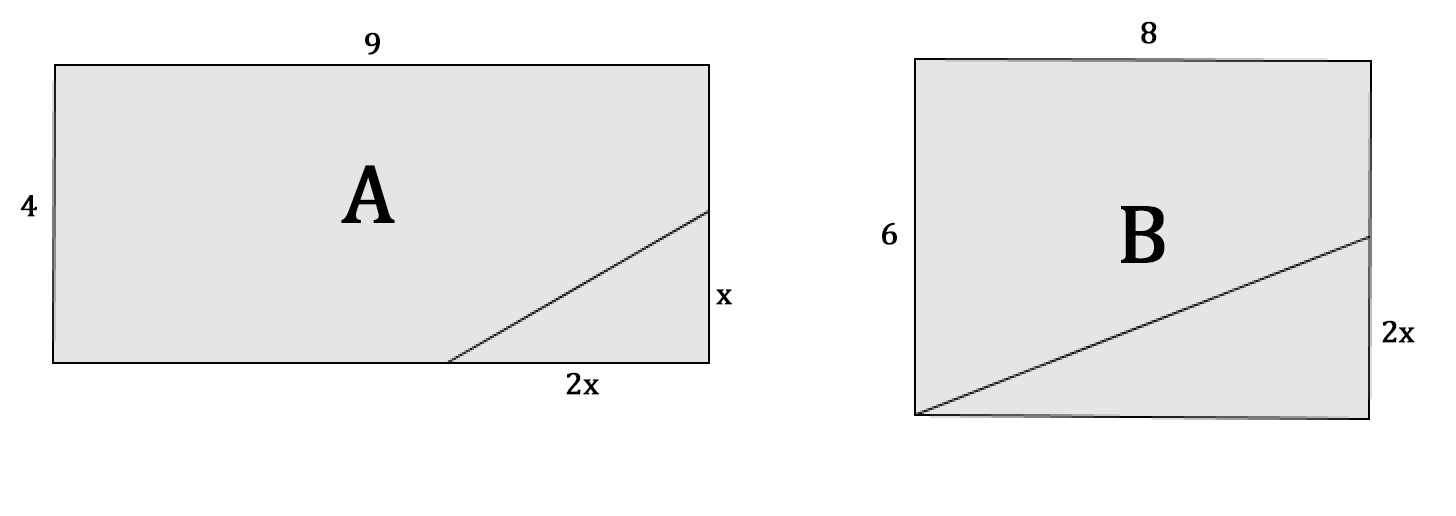
-
Exprimer l'aire A en fonction de x. Factoriser l'expression obtenue.
Vous connaissez tous la formule de l'aire d'un rectangle ? On applique donc la formule.
L'aire de la partie A sera l'aire du rectangle moins l'aire du triangle en bas à droite.
A = 9 × 4 - (x × 2x / 2)
A = 36 - (2x2 / 2)
A = 36 - x2
On identifie de suite une identité remarquable de la forme :a2 - b2 = (a - b)(a + b)
Ce qui donne :
A = 62 - x2
A = (6 - x)(6 + x) -
Exprimer l'aire B en fonction de x. Factoriser l'expression obtenue.
On fait la même chose que la question précédente.
L'aire de la partie B sera l'aire du rectangle moins l'aire du triangle en bas à droite.
B = 8 × 6 - (8 × 2x / 2)
B = 48 - (16x/ 2)
B = 48 - 8x
En remarquant que le chiffre 8 est un facteur commun, on factorise comme ceci :
B = 8(6 - x) -
Pour quelle(s) valeur(s) de x les aires A et B sont-elles égales ?
Les aires A et B sont égales si et seulement si :
A = B ⇔ (6 - x)(6 + x) = 8(6 - x)
On fait tout passer à gauche.
A = B ⇔ (6 - x)(6 + x) - 8(6 - x) = 0
On factorise le tout par le facteur commun apparant (6 - x).
A = B ⇔ (6 - x)(6 + x - 8) = 0
A = B ⇔ (6 - x)(x - 2) = 0
Un produit est nul si et seulement si un de ses facteurs est nul.
A = B ⇔ 6 - x = 0 OU x - 2 = 0
A = B ⇔ x = 6 OU x = 2
Donc, les aires A et B sont-elles égales pour x = 6 ou x = 2.
|
|
Herilaljohn • il y a 4055 jours. Merci pour les exercices |




