On considère une suite arithmétique (un) de premier terme u1 = 1 et de raison r = -2.
-
Calculer les cinq premiers termes de cette suite.
C'est une suite arithmétique. Donc : un + 1 = un + r.
u1 = 1
u2 = u1 - 2 = 1 - 2 = -1
u3 = u2 - 2 = - 1 - 2 = -3
u4 = -5
u5 = -7
u6 = -9 -
Calculer u20.
Utilisons encore une fois la formule de la suite arithmétique.
u20 = u3 + (20 - 3) × ( - 2) = - 3 - 34 = -37 -
Calculer la somme des 20 premiers termes de cette suite.
On utilise la formule du cours tout simplement.
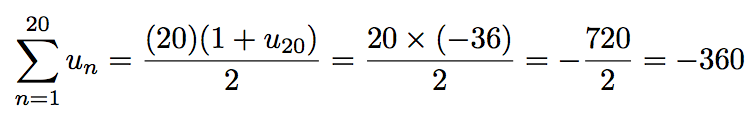
Oui, attention, il y a 20 termes, donc on remplace le (n + 1) de la formule par un n car cela représente le nombre de terme.



