Soit la suite numérique un définie par : un = 5 - 2n
-
Calculer les cinq premiers termes de cette suite.
u0 = 5
u1 = 3
u2 = 1
u3 = -1
u4 = -3 -
Représenter graphiquement la suite un.
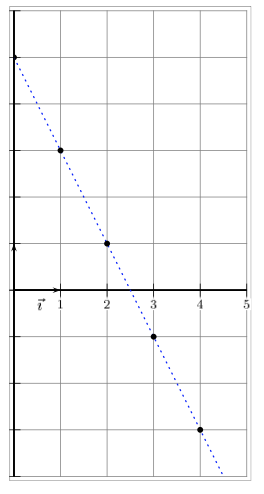
-
Conjecturer que cette suite est arithmétique dont on précisera la raison.
On remarque que la différence de deux termes consécutifs de la suite est constante et égale à -2.
Donc, c'est une suite arithmétique de raison r = -2. -
Calculer u100.
Comme c'est une suite arithmétique, on applique une des deux formules au choix :
u100 = u0 + 100 × (-2) = 5 + 100 × (-2) = 5 - 200 = -195
Ou bien :u100 = u1 + (100 - 1) × (-2) = 3 + 99 × (-2) = 3 - 198 = -195. -
Calculer la somme des 100 premiers termes de cette suite.
Encore une fois, on applique la formule du cours, mais attention, les 100 premiers termes en comptant le u0, cela veut dire jusqu'au u_99.
u99 = u0 + 99 × (-2) = 5 - 198 = - 193
Donc :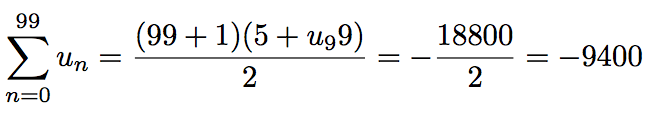
-
Donner les variations de cette suite.
On a :
un = 5 - 2n
un + 1 = 5 - 2(n + 1) = 5 - 2n - 2 = 3 - 2n
Or, on sait très bien que :un = 5 - 2n > 3 - 2n = un + 1
Donc, la suite est décroissante.
D'ailleurs, cela se voyait très bien lorsque l'on a calculé les premiers termes de la suite.



