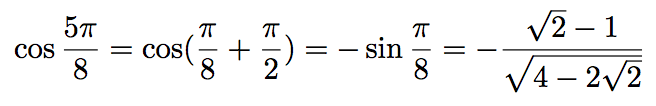On rappelle que tan x = sin x/cos x.
Donnée : tan (π/8) = √2 - 1.
Donnée : tan (π/8) = √2 - 1.
-
Montrer que pour tout
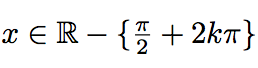 ,
,
tan(π + x) = tan x
En déduire la valeur exacte de tan(9π/8).On a :
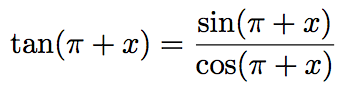
Or, sin (π + x) = -sin x et cos (π + x) = -cos x.
Donc :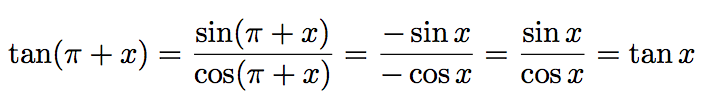
Calculons tan(9π/8).
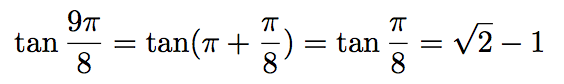
-
Montrer que pour tout
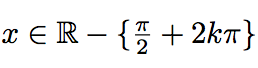 ,
,
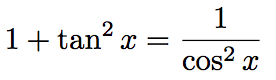
En déduire la valeur exacte de cos(π/8) et de sin(π/8).On a :
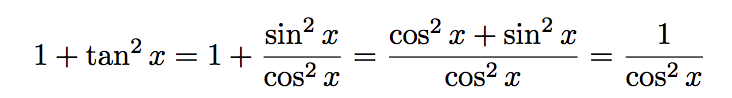
Déduisons-en la valeur exacte de cos(π/8) et de sin(π/8).
Commençons par cos(π/8), la valeur de sin(π/8) se trouvera facilement après.
Utilisons la formule que l'on vient de démontrer.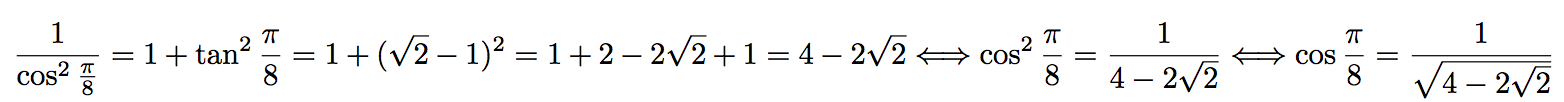
Et pour le sinus :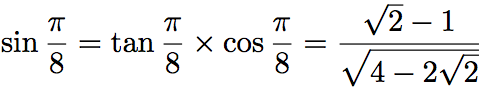
-
Calculer la valeur exacte de cos(5π/8).
On sait que : (5π/8) = (π/8) + (π/2).
De plus, cos(x + π/2) = -sin x.
Donc :