On se propose de résoudre l'équation (E) d'inconnue x ∈ [0; π/2] suivante : cos x + sin x = √2.
-
Donner la solution évidente de (E).
Les solutions évidentes de (E) sont : x = π/4.
-
Première méthode :
Diviser chaque membre de l'équation (E) par √2 puis transformer le premier membre de l'équation.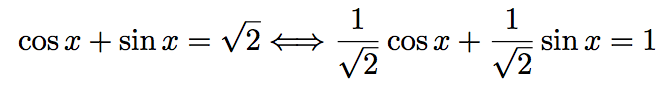
Or, on sait que :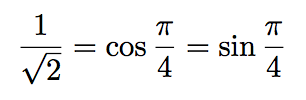
Donc :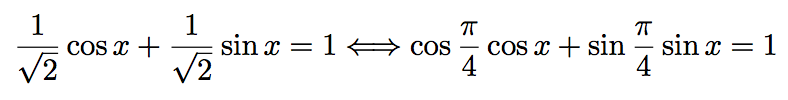
D'après la formule trigonométrique : cos (a - b) = cos a cos b + sin a sin b, on a :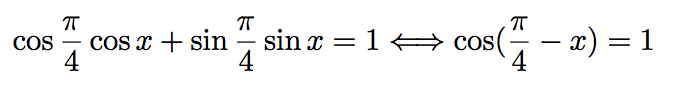
De plus, on sait très bien que : cos 0 = 1.
Donc :cos (π/4 - x) = cos 0 = 1
D'où :(π/4) - x = 0 ⇔ x = π/4
On retrouve bien le résultat prévu de la première question. -
Deuxième méthode :
Poser X = cos x et Y = sin x.
En ajoutant une équation supplémentaire toujours vérifiée par X et Y, former un système de deux équations à deux inconnues que l'on résoudra.On a :
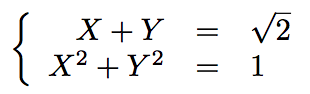
Elevons au carré la première équation trigonométrique.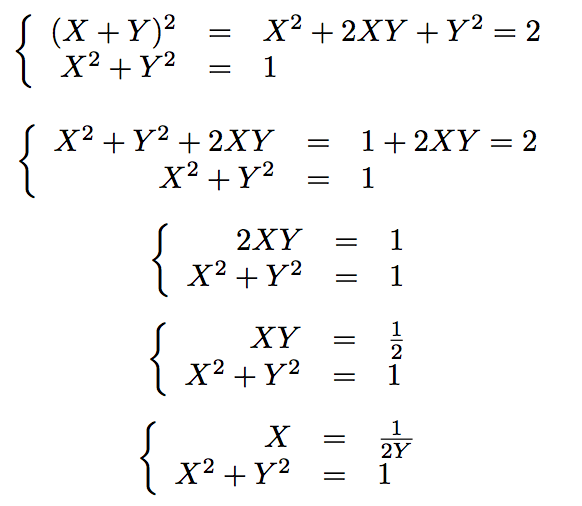
On insère la première équation dans la seconde pour obtenir, après calculs, le polynôme suivant : 4Y4 - 4Y² + 1 = 0.
En effectuant le changement de variable Z = Y², on obtient que : Z = 1/2 et donc que Y = 1/√2. D'où :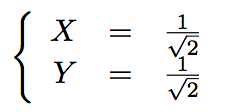
Donc :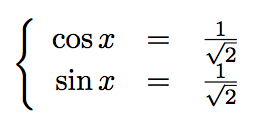
Ce qui veut dire que : x = π/4.
On retrouve encore une fois le résultat de la question 1. -
Troisième méthode :
En développant (cos x + sin x)², justifier que sur [0; π/2], l'équation (E) équivaut à l'équation suivante que l'on résoudra : sin(2x) = 1.On a :
cos x + sin x = √2 ⇔ (cos x + sin x)² = 2 ⇔ cos² x + sin² x + 2sin x cos x = 2
Comme cos² x + sin² x = 1,1 + 2sin x cos x = 2 ⇔ 2sin x cos x = 1
De plus, 2sin x cos x = sin(2x).
Donc, résoudre l'équation (E) revient à résoudre l'équation suivante :sin(2x) = 1
Que l'on résous aisément en sachant que sin (π/2) = 1.sin(2x) = sin (π/2) = 1
Donc :2x = π/2 ⇔ x = π/4
Encore une fois, on confirme bien la réponse de la question 1.
Quelle méthode préférez - vous ?
Il faut quand même que vous sachiez faire les trois !



