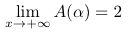Soit un repère orthonormé d'unité 2cm. On considère la fonction f définie sur R par :
f(x) = 2 x + 1 - xe-x²
-
Démontrer que la courbe représentative de la fonction f admet la droite (D), d'équation y = 2x + 1, comme asymptote au voisinage de +∞. Etudier la position relative des deux courbes.
Calculons la limite suivante :
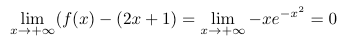
De là, on en déduit que Cf admet bien la droite (D) d'équation y = 2x + 1, comme asymptote au voisinage de +∞.
Etudions la position relative de la fonction f par rapport à son asymptote.
Pour tout réel x, on a :
f(x) - (2x + 1) = -xe-x²
De plus, on sait qu'une exponentielle est toujours positive, donc :
e-x² > 0
Donc, pour tout x > 0 :
f(x) - (2x + 1) = -xe-x² < 0
Et pour tout x < 0 :
f(x) - (2x + 1) = -xe-x² > 0
Conclusion : sur ]0; +∞[, Cf est en-dessous de (D) et sur ]-∞; 0[, Cf est au-dessus de (D). -
Soit α > 0. On note A(α) l'aire du domaine délimité par les droites d'équation x = 0, x = α, et les courbes d'équation y = f(x) et y = 2x + 1.
Calculer A(α) en fonction de α puis déterminer la limite de A(α) quand α tend vers +∞.On vient de voir que sur ]0; +∞[, Cf est en-dessous de (D).
Donc, l'aire du domaine recherché est :
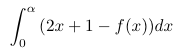
On calcule cette intégrale de la façon suivante :
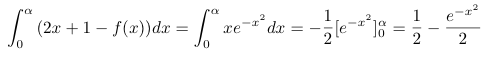
Finalement, l'aire en cm² est :
A(α) = 2 - 2e-α²
Calculons la limite en l'infini.
On sait que :
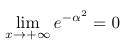
Donc :