Terminons ce chapitre sur les dérivées par un cours sur l'approximation affine et tangente à la courbe en un point. Qu'es-ce que c'est ? Je vous explique tout ici.
On peut traduire la notions de dérivée d'une autre façon.
Propriété
Approximation affine
Si f est dérivable en a, alors f(x) = (x - a)f'(a) + f(a) + (x - a)ε(x) avec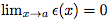 .
.
On appelle approximation affine de f :
C'est quoi ce "ε" ?
Il se lit "Espilon", c'est une lettre grecque.
Cette propriété signifie que lorsque x est proche de a, alors une approximation de f(x) est (x - a)f'(a) + f(a).
La quantité (x - a) ε(x) représente en fait l'erreur commise lorsque l'on remplace f(x) par (x - a)f'(a) + f(a).
Introduisont à présent la notion de tangente à la courbe.
Soit f une fonction représentée par la courbe 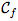 .
.
Soit M0(x0 ; f(x0)) un point de 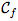 .
.
Soit M(x ; f(x)) un point de 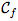 .
.
Soit Δx la droite passant par M0 et M.
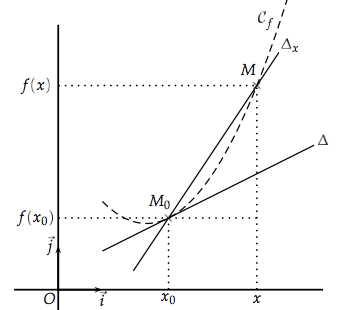
Quand x s'approche de x0, alors la droite Δx pivote autour du point M0 et le point M glisse sur la courbe
 vers le point M0.
vers le point M0.
Quand x est très proche de x0, c'est-à-dire quand x tend vers x0, la droite Δx bascule alors vers une droite limite Δ qu'on appelle tangente à la courbe
 au point M0.
au point M0.
Le coefficient directeur de la droite Δx est :
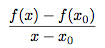
Alors le coefficient directeur de la droite Δ est :
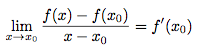
Vous retiendrez la chose suivante :
On vient de parler de tangente à la courbe sans même l'avoir définit. Rattrapons-nous en la définissant maintenant !
Définition
Equation de la droite tangente à la courbe en un point
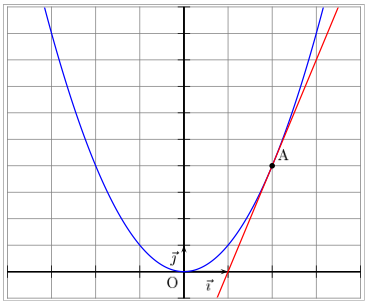
L'équation de la droite tangente à la courbe au point M0 d'abscisse x0 est :Exemple
En effet :
Car la dérivée de la fonction carré est la fonction f '(x) = 2x.
Il faut toujours que le point où l'on calcule la tangente appartienne à la courbe ?
Non, pas du tout. On calcule la tangente en un point désigné par son abscisse uniquement.
|
|
• il y a 820 jours. 0 |
|
|
• il y a 820 jours. 0 |
|
|
• il y a 820 jours. 0 |
|
|
• il y a 820 jours. 0 |
|
|
• il y a 820 jours. 0 |




