Déterminer une équation cartésienne d'une droite, ce n'est pas si simple. Je vous montre comment faire, avec un point et un vecteur directeur d'une droite.
Déterminer une équation cartésienne de la droite passant par A(2; -1) et de vecteur directeur 
(-3; 4).
Donner la forme d'une équation de droite
D'après le cours (que l'on connait par coeur évidemment), on sait qu'une équation cartésienne de droite est de la forme : ax + by + c = 0.
Déterminer un vecteur directeur de la droite
Pour obtenir un vecteur directeur de la droite, plusieurs façons possibles :
- Soit il est donné dans l'énoncé.
- Soit on donne deux points A et B appartenant à (d),
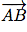est alors un vecteur directeur de (d). - Soit on donne une droite parallèle à la droite (d) de vecteur directeur connu. Un vecteur directeur de (d) est égal au vecteur directeur de la droite parallèle.
Là, on a de la chance, l'énoncé nous donne le vecteur directeur. En effet, la droite a pour vecteur directeur (-3; 4).
Déterminer les valeurs de a et b de l'équation de la droite
On sait que si (-b; a) est un vecteur directeur la droite (d), alors (d) admet une équation de la forme ax + by + c = 0.
On détermine donc les valeurs de a et de b.
On sait que (d) a une équation de la forme ax + by + c = 0.
Or (-3; 4) est un vecteur directeur de (d).
On peut choisir a et b tels que :
a = 4
b = 3
a = 4
Ainsi (d) admet une équation cartésienne comme suit : 4x + 3y + c = 0.
Donner les coordonnées d'un point de la droite
Avec l'énoncé, on a les coordonnées d'un point A(xA; yA) de la droite (d).
Le point A(2; -1) appartient à la droite (d).
Déterminer la valeur de c
Il ne reste plus qu'à déterminer c.
On sait que le point A(xA; yA) appartient à la droite (d). Ses coordonnées vérifient donc les équations de (d).
On remplace donc dans l'équation précédente de la droite :
On connaît a, b, xA et yA, on peut donc déterminer c.
La droite (d) passe par le point A(2; -1). Donc les coordonnées de A vérifient l'équation précédente de (d).
Ainsi :
4 × 2 + 3 × (-1) + c = 0
8 - 3 + c = 0
c = -5
Conclusion
En remplaçant les valeurs trouvées de a, b et c, on obtient une équation cartésienne de (d) :