Définition et propriétés sur les fonctions concaves pour être prêt pour le bac. Comment montre-t-on qu'une fonction est concave, vous apprendrez tout cela dans cette partie du cours sur la convexité.
On passe à présent aux fonction concaves. Vous l'aurez compris je pense, c'est la même chose mais à l'envers on va dire.
Définition
Fonction concave
Une fonction est concave sur un intervalle I si sa courbe représentative est intégralement située en-dessous de chacune de ses tangentes sur I.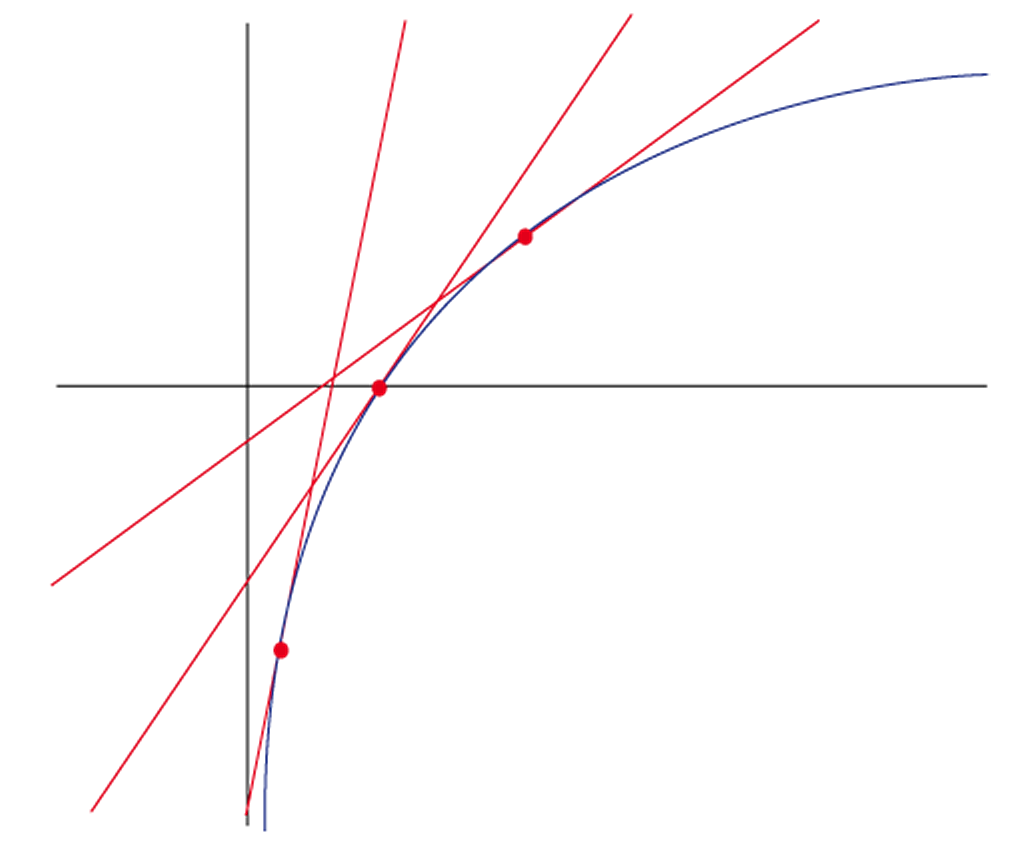
Là aussi, la figure explique tout.
Je vous donne un exemple.
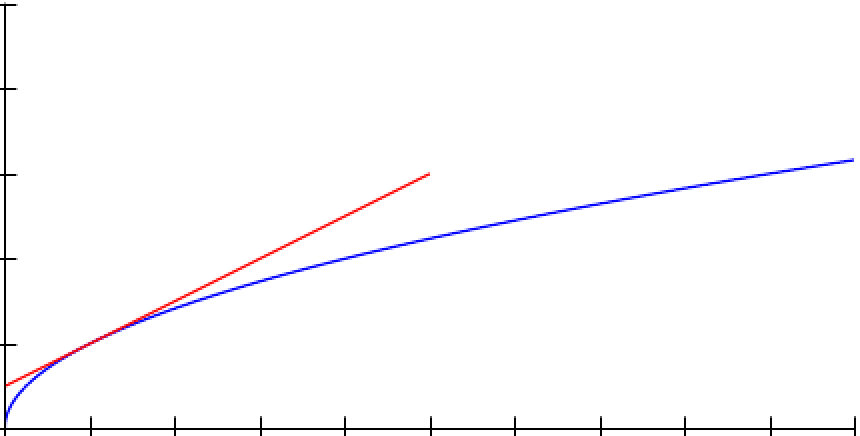
La fonction racine carrée f(x) = √x est une fonction concave.

Encore une fois : comment démontre-t-on qu'une fonction est concave ? Avec les dérivées aussi ?
Oui, encore avec les dérivées.
Propriétés
Propriétés des fonctions concaves
Soit f une fonction dérivable sur un intervalle I.- La fonction f est concave sur I si et seulement si sa dérivée f' est décroissante sur I.
- La fonction f est concave sur I si et seulement si sa dérivée seconde f'' est négative sur I.
Pour savoir si une fonction est concave, il faut donc calculer sa dérivée première et, si celle-ci est décroissante, autrement dit si la dérivée de cette dérivée (la dérivée seconde donc) est négative, la fonction est concave sur l'intervalle donné.





