Un cours de maths sur les fonctions convexes. Dans cette partie, nous vous expliquons ce qu'est une fonction convexe, qu'est ce qui la caractérise et surtout comment la démontre-t-on.
On commence par la fonction convexe, avec une définition avant la propriété.
Définition
Fonction convexe
Une fonction est convexe sur un intervalle I si sa courbe représentative est intégralement située au-dessus de chacune de ses tangentes sur I.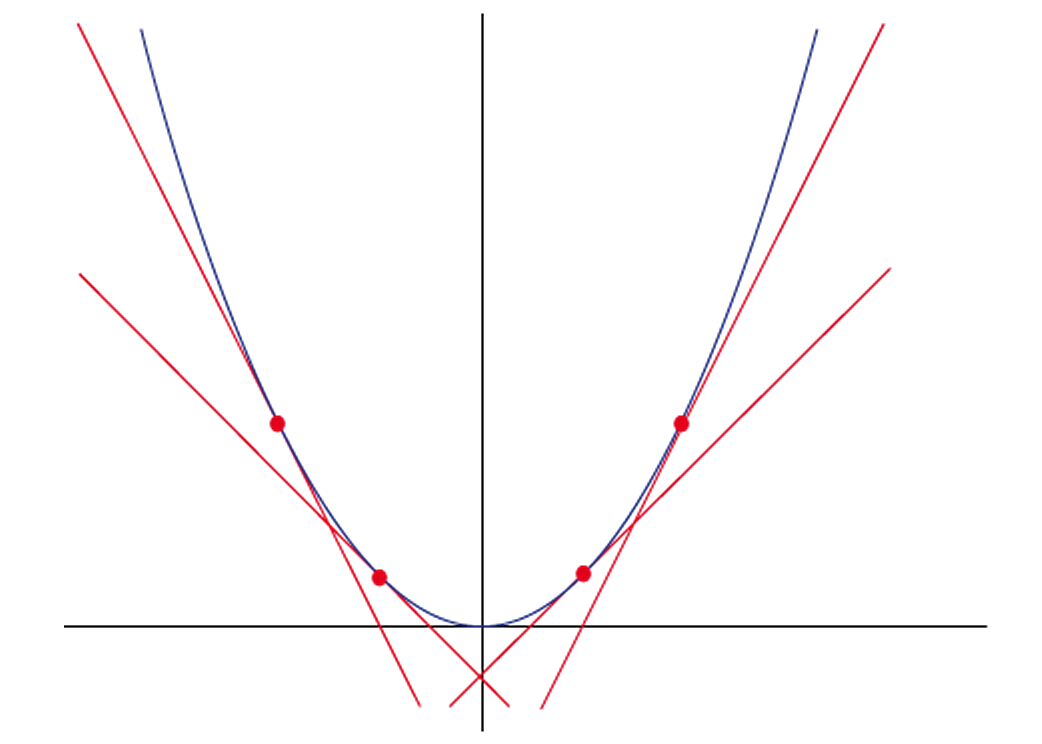
Je pourrai tout expliquer, mais je pense que la figure est très claire.
Je vais quand même vous donner un exemple que vous connaissez tous.
Exemple
La fonction carrée f(x) = x2 est une fonction convexe.
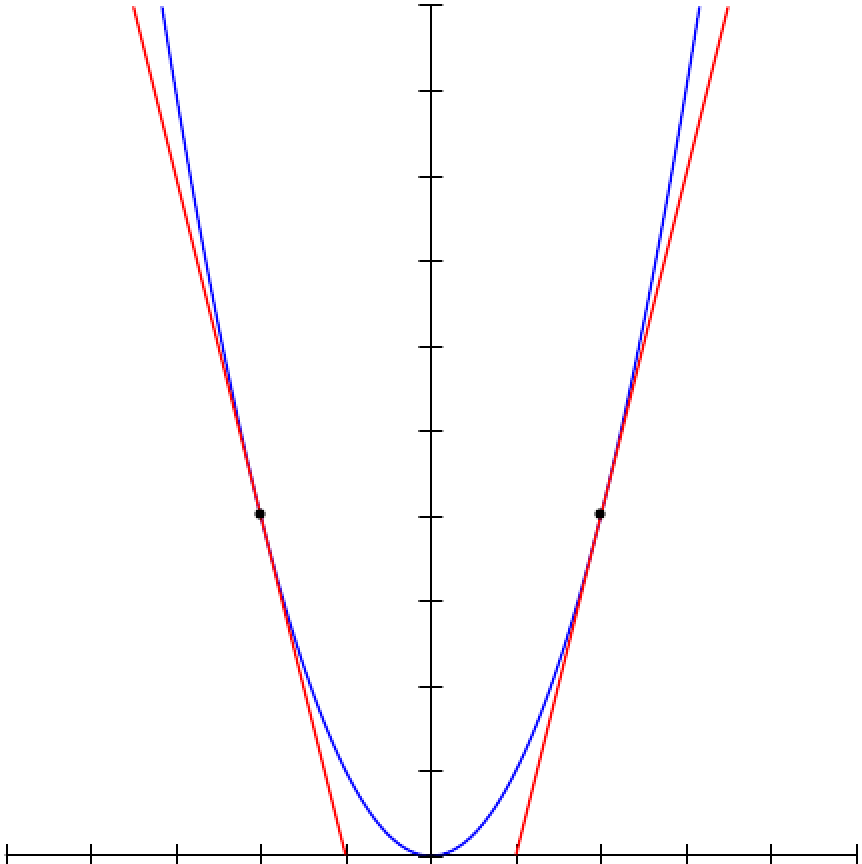

Et sans la courbe, comment on démontre qu'une fonction est convexe ?
C'est avec les dérivées première et seconde. J'y viens tout de suite avec ces deux propriétés.
Propriétés
Propriétés des fonctions convexes
Soit f une fonction dérivable sur un intervalle I.- La fonction f est convexe sur I si et seulement si sa dérivée f' est croissante sur I.
- La fonction f est convexe sur I si et seulement si sa dérivée seconde f'' est positive sur I.
Donc, pour savoir si une fonction est convexe, il faut calculer sa dérivée première et, si celle-ci est croissante, autrement dit si la dérivée de cette dérivée (la dérivée seconde donc) est positive, la fonction est convexe sur l'intervalle donné.





