Résolution d'une équation trigonométrique

Cours terminale S

Dans ce cours méthode, nous allons, ensemble, en utilisant les formules trigonométriques, résoudre l'équation trigonométrique (E) d'inconnue x ∈ [0; π/2] suivante :

cos x + sin x = √2.

Je vais vous donner trois méthodes différentes pour résoudre cette équation trigonométrique. Ces trois méthodes ne sont pas toujours possibles mais cela vous montre qu'ils existent plusieurs façons de faire.

Déterminer une solution évidente de (E)

En cherchant bien et en essayant avec des valeurs logiques, on peut trouver une solution évidente de l'équation (E). Je vous l'accorde, ce n'est pas toujours le cas. Souvent, quand c'est possible et facilement trouvable, c'est demandé dans l'énoncé.

Ici, les solutions évidentes de (E) sont : x = π/4. Je vous laisse vérifier.

Première méthode

Cette première méthode consiste à diviser chaque membre de l'équation (E) par √2 puis transformer le premier membre de l'équation.

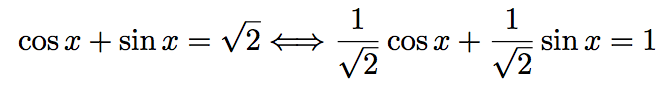
Or, nous savons que (enfin, si on connait son cours!) :

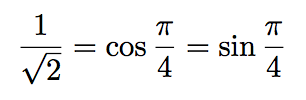
Donc :

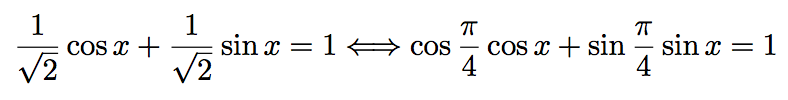
D'après la formule trigonométrique : cos (a - b) = cos a cos b + sin a sin b, on a :

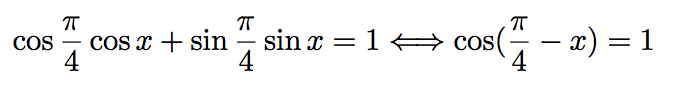
De plus, on sait très bien que : cos 0 = 1.
Donc :

cos (π/4 - x) = cos 0 = 1

D'où :

(π/4) - x = 0 ⇔ x = π/4

On retrouve bien le résultat prévu de la première question.

Deuxième méthode

Maintenant, nous allons poser X = cos x et Y = sin x. En ajoutant une équation supplémentaire toujours vérifiée par X et Y, former un système de deux équations à deux inconnues que l'on résoudra.

On a :

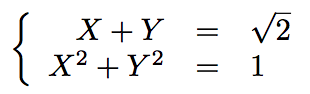
Elevons au carré la première équation trigonométrique.

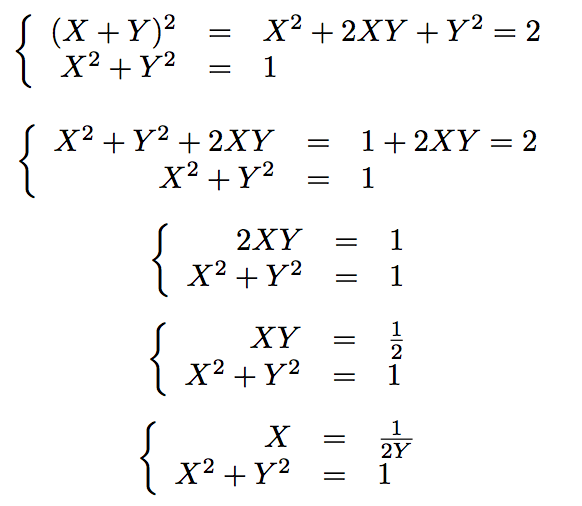
On insère la première équation dans la seconde pour obtenir, après calculs, le polynôme suivant : 4Y⁴ - 4Y² + 1 = 0.

En effectuant le changement de variable Z = Y², on obtient que : Z = 1/2 et donc que Y = 1/√2.

D'où :

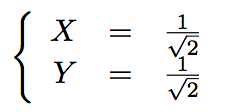
Donc :

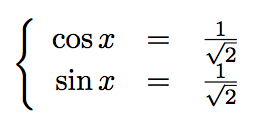
Ce qui veut dire que : x = π/4. On retrouve encore une fois le résultat de la question 1.

Troisième méthode

En développant (cos x + sin x)², justifier que sur [0; π/2], l'équation (E) équivaut à l'équation suivante que l'on résoudra : sin(2x) = 1.

On a :

cos x + sin x = √2 ⇔ (cos x + sin x)² = 2 ⇔ cos² x + sin² x + 2sin x cos x = 2

Comme cos² x + sin² x = 1,

1 + 2sin x cos x = 2 ⇔ 2sin x cos x = 1

De plus, 2sin x cos x = sin(2x).

Donc, résoudre l'équation (E) revient à résoudre l'équation suivante :

sin(2x) = 1

Que l'on résous aisément en sachant que sin (π/2) = 1.

sin(2x) = sin (π/2) = 1

Donc :

2x = π/2 ⇔ x = π/4

Encore une fois, on confirme bien la réponse de la question 1.