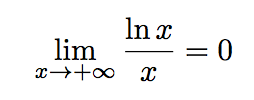On pose, pour tout x ∈ ]0;+∞[ :
f(x) = 2√x - ln(x)
-
Montrer que f admet un minimum en x = 1.
La fonction f est dérivable sur
 *+.
*+.
Dérivons la :
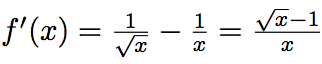
La dérivée s'annule pour x = 1.
Déterminons à présent s'il s'agit d'un maximum ou d'un minimum.
Pour x > 1, on a une dérivée positive et donc une fonction strictement croissante.
Pour 0 < x < 1, la dérivée est négative et donc la fonction est strictement décroissante.
Conclusion : la fonction f admet un minimum en x = 1. -
En déduire que si x ≥ 1, alors 0 ≤ ln x ≤ 2 √x.
On sait que le minimum de la fonction f est atteint pour x = 1 et donc que f (1) = 2.
Donc, la fonction f est strictement positive car sa valeur minimale est 2.
D'où :
f(x) > 0
⇔ 2√x - ln(x) > 0
⇔ 2√x > ln(x)
Et si x ≥ 1,
0 ≤ ln(x) ≤ 2√x -
En déduire la limite suivante :
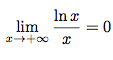 .
.Utilisons encore une fois la question précédente : si x ≥ 1, alors 0 ≤ ln(x) ≤ 2√x.
Divisons tous les termes par x :
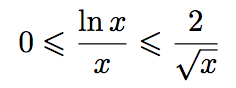
Or,
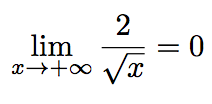
Donc, d'après le théorème des gendarmes :