Soit la fonction f définie par :
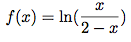
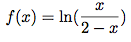
-
Quel est l'ensemble de définition de la fonction f ?
Il faut nécessairement que ce que "mange" le ln soit strictement positif.
Soit : x/(2 - x) > 0 ⇔ 0 < x < 2
Donc : Df = ]0; 2[. -
Calculer la dérivée de la fonction f.
La fonction f est dérivable sur son ensemble de définition et sa dérivée vaut :
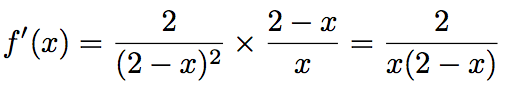
-
Déterminer une équation de la tangente (T) à la courbe représentative de la fonction f au point d'abscisse 1.
D'abord, es-ce que cette tangente existe ? Oui, car la fonction f est dérivable en 1.
L'équation de la tangente (T) à la courbe représentative de la fonction f au point d'abscisse 1 a pour équation :
y = f'(1) × (x - 1) + f(1)
⇔ y = 2x - 2 -
Etudier la position relative de la courbe représentative de la fonction f et de la droite (T).
Posons, pour tout x ∈ Df, la fonction g(x) = f(x) - y = f(x) - y.
Le signe de cette fonction va nous aider à répondre à la question.
Calculons sa dérivée.
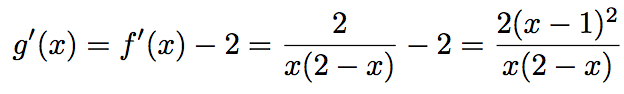
Pour tout x ∈ Df et différent de 1, g' (x) > 0. La fonction g est strictement croissante sur Df.
Comme (T) est la tangente à (C) au point d'abscisse 1, on a : g(1) = 0.
Si 0 < x < 1, alors g(x) < 0 et si 1 < x < 2 alors g(x) > 0.
Conclusion :
- Sur ]0; 1[, la courbe (C) est en dessous de la droite (T).
- Sur ]1; 2[, la courbe (C) est au dessus de la droite (T).




