Résoudre les équations suivantes :
-
ln(1 + x) = ln(1 - 2x)
ln(1 + x) = ln(1 - 2x)
⇔ 1 + x = 1 - 2x
⇔ x = 0 -
ln(3 + x) + ln(3 - x) = ln5
Il faut nécessairement que 3 + x > 0 et 3 - x > 0, c'est-à-dire que x > 3.
ln(3 + x) + ln(3 - x) = ln5
⇔ ln[(3 + x)(3 - x)] = ln5
⇔ ln(x² - 9) = ln5
⇔ x² - 9 = 5
⇔ x = √14 -
ln(3 + x) - ln(x + 13) + ln(x + 1) = 0
Il faut nécessairement que x + 1 > 0, que 3 + x > 0 et que x + 13 > 0.
Autrement dit, l'ensemble de définition de l'équation est : ]-1; +∞[.
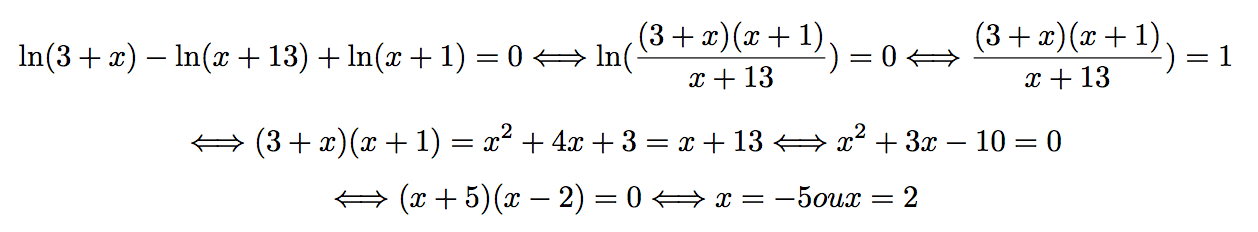
Or, -5 < -1 et 2 > -1. Il n'y a que la solution 2 qui est dans l'ensemble de définition.
Conclusion : x = 2 est l'unique solution de l'équation.
Remarque : vous voyez bien l'utilité de trouver le domaine de définition. -
2ln³(x) + 5ln²(x) + ln(x) - 2 = 0
Exemple un tout petit peu plus difficile.
L'équation est définie pour x > 0.
On remarque très vite qu'un ressemble à une équation polynomiale.
Posons donc : X = ln x.
L'équation devient : 2X³ + 5X² + X - 2 = 0.
En cherchant une racine évidente (rapidement, de tête), on remarque que -1 en est une.
Factorisons donc ce polynôme par -1 :
2X³ + 5X² + X - 2 = 0 ⇔ (X + 1)(2X² + 3X - 2) = 0
Le discriminant du polynôme 2X² + 3X - 2 vaut : Δ = 25.
Ces racines sont donc les suivantes :
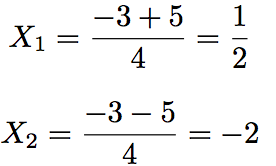
Revenons à l'équation polynomiale du départ.
2X³ + 5X² + X - 2 = 0 ⇔ (X = -1 ou X = 1/2 ou X = -2)
En revenant aux ln :
ln(x) = -2 ou ln(x) = -1 ou ln(x) = 1/2
Ce qui équivaut à :
x = 1/e² ou x = 1/e ou x = √e
Conclusion : S = {1/e²; x = 1/e; √e}




