Le gros de ce cours de maths réside dans cette partie sur les vecteurs. Au programme : définition, somme de deux vecteurs, vecteurs opposés, translations et bien d'autres nouveautés.
1 - Définition des vecteurs
On va parler dans cette section de vecteurs dans un repère. Commençons par une définition.
Définition
Vecteurs
Soit un vecteur .
.
Lorsque l'on construit l'image de l'origine O du repère par la translation de vecteur
 , on obtient un point, que nous appellerons A, qui a les mêmes coordonnées que le vecteur
, on obtient un point, que nous appellerons A, qui a les mêmes coordonnées que le vecteur  .
.
On note :
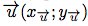 .
.
Je vous donne un exemple.
Exemple
Soient deux vecteurs  (4, 2) et
(4, 2) et 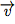 (-2; -3).
(-2; -3).
Cela signifie que le vecteur fait 4 pas à droite et 2 pas en haut et le vecteurs
fait 4 pas à droite et 2 pas en haut et le vecteurs 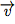 fait 2 pas à gauche et 3 pas en bas.
fait 2 pas à gauche et 3 pas en bas.
Regardez le graphique suivant, on a représenté le vecteur et construit l'image de l'origine O du repère par la translation de vecteur
et construit l'image de l'origine O du repère par la translation de vecteur  .
.
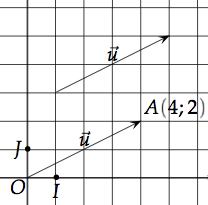
Cela nous donne le point A de même coordonnées que le vecteur : A(4; 2).
: A(4; 2).
 (4, 2) et
(4, 2) et 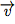 (-2; -3).
(-2; -3).
Cela signifie que le vecteur
 fait 4 pas à droite et 2 pas en haut et le vecteurs
fait 4 pas à droite et 2 pas en haut et le vecteurs 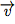 fait 2 pas à gauche et 3 pas en bas.
fait 2 pas à gauche et 3 pas en bas.
Regardez le graphique suivant, on a représenté le vecteur
 et construit l'image de l'origine O du repère par la translation de vecteur
et construit l'image de l'origine O du repère par la translation de vecteur  .
.
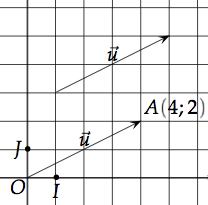
Cela nous donne le point A de même coordonnées que le vecteur
 : A(4; 2).
: A(4; 2).
Remarque
Pour construire l'image du point B quelconque par la translation de vecteur  (6; -2), on va partir du point B et monter de 2 pas vers le bas et aller 6 pas vers la droite.
(6; -2), on va partir du point B et monter de 2 pas vers le bas et aller 6 pas vers la droite.
 (6; -2), on va partir du point B et monter de 2 pas vers le bas et aller 6 pas vers la droite.
(6; -2), on va partir du point B et monter de 2 pas vers le bas et aller 6 pas vers la droite.
2 - Vecteur défini par deux points
Je vais vous apprendre à calculer les coordonnées d'un vecteur à partir de deux points : son point de départ et son point d'arrivée.
Propriété
Vecteur défini par deux points
Soient A(xA; yA) et B(xB; yB).Le vecteur
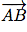 a pour coordonnées :
a pour coordonnées :
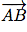 (xB - xA; yB - yA)
(xB - xA; yB - yA)Exemple
Calculons les coordonnées du vecteur formé par les points A(4; 6) et B(-1; 2).
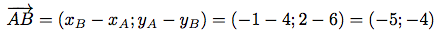
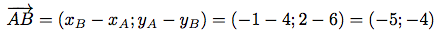
3 - Somme de deux vecteurs
On peut également sommer deux vecteurs.
Propriété
Somme de deux vecteurs
Soient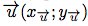 et
et 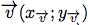 .
.
Les coordonnées de la somme des vecteurs
 et
et 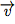 est :
est :
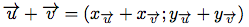
Exemple
Calculons les coordonnées de la somme des vecteurs  (4; -2) et
(4; -2) et 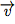 (0; 3).
(0; 3).
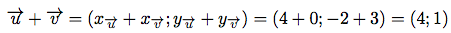
 (4; -2) et
(4; -2) et 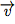 (0; 3).
(0; 3).
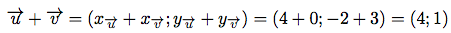
4 - Vecteurs opposés
On redéfini le vecteur opposé au sens des coordonnées.
Définition
Vecteurs opposés
Soit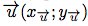 .
.
Le vecteur opposé au vecteur
 est le vecteur :
est le vecteur :
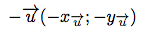
5 - Vecteur nul
Vous imaginer bien sur à quoi va ressembler le vecteur nul.
Définition
Vecteurs nul
Les coordonnées du vecteur nul sont :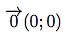
6 - Translation
Et la translation au sens des coordonnées, cela donne quoi ?
Propriété
Translation
Soient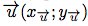 et A(xA; yA).
et A(xA; yA).
Soit A', l'image de A par la translation de vecteur
 .
.
Les coordonnées de A' sont :
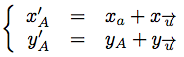
Donnons un exemple.
Exemple
Soient  (6; -1) et A(5; 4). Calculons les coordonnées du point A', image du point A par la translation de vecteur
(6; -1) et A(5; 4). Calculons les coordonnées du point A', image du point A par la translation de vecteur  .
.
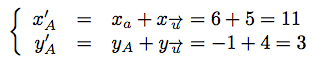
On a donc : A'(11; 3).
 (6; -1) et A(5; 4). Calculons les coordonnées du point A', image du point A par la translation de vecteur
(6; -1) et A(5; 4). Calculons les coordonnées du point A', image du point A par la translation de vecteur  .
.
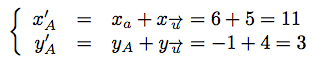
On a donc : A'(11; 3).




