Le théorème fondamentale de la géométrie en 4ème : le théorème de Pythagore. Dans ce cours, je vous énonce le théorème et l'applique sur des exemples simple.
Je vais vous apprendre ce fameux théorème dont tout le monde parle : le théorème de Pythagore. Il va vous servir à calculer la longueur d'un côté d'un triangle rectangle à partir des longueurs des deux autres. Pratique, non ?
Théorème
Théorème de Pythagore
Soit un triangle ABC, rectangle en A.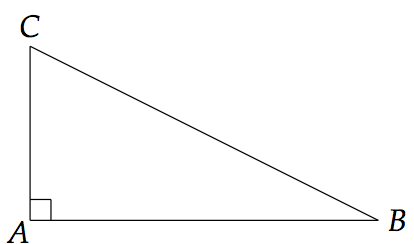
D'après le théorème de Pythagore, on a :
Ce qui veut dire que la longueur de l'hypoténuse élevée au carré est égale à la somme des carrés des deux autres côtés du triangle.
Attention
Il faut absolument avoir un triangle rectangle.
Exemple
Soit le triangle RST rectangle en R suivant :
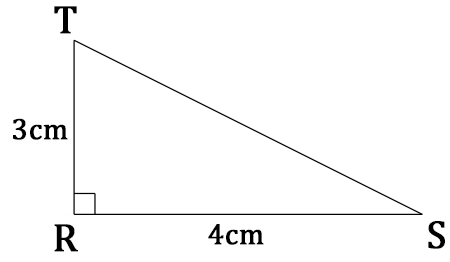
Dans ce triangle, on a RS = 4cm et RT = 3cm.
Calculer TS.
On a ici un triangle rectangle. On peut donc appliquer le théorème de Pythagore.
Donc, dans le triangle RST, rectangle en R, d'après le théorème de Pythagore :
TS² = RS² + RT²
Or, RS = 4cm et RT = 3cm.
Donc, on peut faire l'application numérique :
TS² = RS² + RT² = 4² + 3² = 16 + 9 = 25
Oui mais là on obtient la longueur du côté au carré. Comment revient-on à la longueur du côté ?
On fait un coup de racine carrée :
TS = √25 = 5cm

Dans ce triangle, on a RS = 4cm et RT = 3cm.
Calculer TS.
On a ici un triangle rectangle. On peut donc appliquer le théorème de Pythagore.
Donc, dans le triangle RST, rectangle en R, d'après le théorème de Pythagore :
Or, RS = 4cm et RT = 3cm.
Donc, on peut faire l'application numérique :
Oui mais là on obtient la longueur du côté au carré. Comment revient-on à la longueur du côté ?
On fait un coup de racine carrée :
Oulala, attendez un peu. Qu'es-ce que c'est que la racine carrée ?
J'attendais cette question. Voici la définition.
Définition
Racine carrée
La racine carrée √a du nombre positif aa est le nombre positif dont le carré est égal à a :
Quand on élève un nombre a au carrée, on obtient a². La racine carrée c'est simplement le sens inverse.
Exemple
Et donc, en faisant le chemin inverse :
Vous aurez plus de précisions l'année prochaine, pour votre Brevet.
Remarque
On peut vous demander, parfois, de calculer la longueur d'un autre côté du triangle rectangle.
Exemple
Soit le triangle IJK, rectangle en I, suivant :
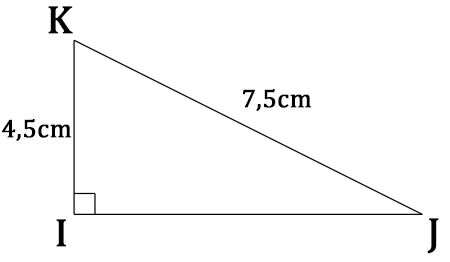
Dans ce triangle, on a IK = 4,5cm et KJ = 7,5cm.
Calculer IJ.
On a ici un triangle rectangle. On peut donc appliquer le théorème de Pythagore.
Donc, dans le triangle IJK, rectangle en I, d'après le théorème de Pythagore :
KJ² = IJ² + IK²
Ce qui veut dire que :
IJ² = KJ² - IK²
Eh oui, c'est une simple équation. Donc en faisant passé un terme de droite à gauche, on change tout simplement son signe.
Or, IK = 4,5cm et KJ = 7,5cm.
Donc, on peut faire l'application numérique :
IJ² = KJ² - IK² = 7,5² - 4,5² = 56,25 - 20,25 = 36
D'où:
IJ = √36 = 6cm

Dans ce triangle, on a IK = 4,5cm et KJ = 7,5cm.
Calculer IJ.
On a ici un triangle rectangle. On peut donc appliquer le théorème de Pythagore.
Donc, dans le triangle IJK, rectangle en I, d'après le théorème de Pythagore :
Ce qui veut dire que :
Eh oui, c'est une simple équation. Donc en faisant passé un terme de droite à gauche, on change tout simplement son signe.
Or, IK = 4,5cm et KJ = 7,5cm.
Donc, on peut faire l'application numérique :
D'où:




