Retrouvez toutes les formules d'aires des figures géométriques que vous avez apprises jusqu'ici : l'aire d'un carré, d'un rectangle, d'un losange, d'un parallélogramme, d'un triangle, l'aire d'un disque et même l'aire d'un trapèze.
Voici les formules d'aires, très utile en géométrie.
Dans toutes ces formules, la lettre 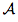 désigne l'aire de la surface étudiée.
désigne l'aire de la surface étudiée.
1 - Aire d'un carré
Soit un carré de côté c.

L'aire de ce carré est défini par :
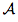 = c × c = c²
= c × c = c²Exemple
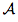 = c² = 3 × 3 = 9cm²
= c² = 3 × 3 = 9cm²
Vous voyez, on ne fait qu'appliquer la formule bêtement. On remplace les lettres de la formule par les chiffres donnés dans l'énoncé de l'exercice.
Maintenant que vous avez compris, je vais vous énumérer les formules d'aires les unes à la suite des autres.
2 - Aire d'un rectangle
Soit un rectangle de largeur l (petit côté) et de longueur L (grand côté).
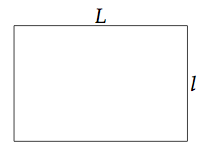
L'aire de ce rectangle est défini par :
 = l × L
= l × L3 - Aire d'un losange
Soit un losange dont la grande diagonale fait une longueur D et la petite fait une longueur d.
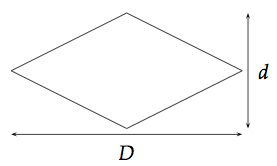
L'aire de ce losange est défini par :
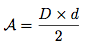
4 - Aire d'un parallélogramme
Soit un parallélogramme de base b et de hauteur h.
Sachez bien que la hauteur est perpendiculaire aux deux bases.
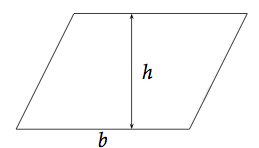
L'aire de ce parallélogramme est défini par :
 = b × h
= b × h5 - Aire d'un triangle
Soit un triangle de base b et de hauteur correspondante h.
Faites bien attention, on prend la hauteur perpendiculaire à la base que l'on utilise.
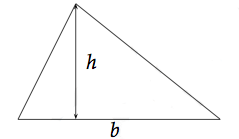
L'aire de ce triangle est défini par :
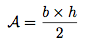
Vous remarquerez que c'est l'aire d'un parallélogramme divisé par deux. Oui, parce-qu'un parallélogramme, c'est tout simplement deux triangles collés.
6 - Aire d'un triangle rectangle
Soit un triangle rectangle de base b et de hauteur correspondante a. Ici, la hauteur correspondante n'est rien d'autre que le second côté du triangle.
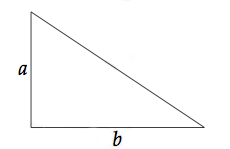
L'aire de ce triangle rectangle est défini par :
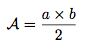
C'est la moitié de l'aire d'un rectangle. Vous comprendrez pourquoi.
7 - Aire d'un trapèze
Soit un trapèze de grande base B, de petite base b et de hauteur h.
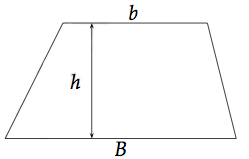
L'aire de ce trapèze est défini par :
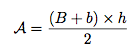
8 - Aire d'un disque
Soit un disque de rayon r.
Oui, on parle bien de disque et non de cercle car le cercle c'est juste la bordure du disque. Ce dernier lui est remplie.
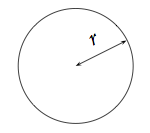
L'aire de ce disque est défini par :
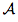 = π × r × r = π × r²
= π × r × r = π × r²


