Commençons ce cours sur les limites de suites numériques par la convergence et la divergence. Dans cette première partie, on plante le contexte pour bien comprendre la suite.
Que peut faire une suite, au fur et à mesure des n croissants?
Réponse :
- Soit tendre vers un réel,
- Soit tendre vers l'infini,
- Soit elle ne tend vers rien.
Définitions
Convergence et divergence de suites
- On dit qu'une suite un converge vers un réel L si pour tout intervalle ouvert U contenant L, tous les termes de la suite appartiennent à U sauf un nombre fini.
On note alors :
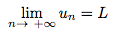
L est la limite de la suite un et elle est unique. - Une suite est divergente si elle n'est pas convergente.
Explication : Si plus on va dans les n grands, plus la suite se rapproche d'un nombre, que l'on va désigné par le réel L, alors on dira que la suite est convergente vers le réel L.
Autrement dit, et en reprenant les termes de la définition, à partir d'un certain rang n, tous les termes de la suites tendent vers le réel L.
Si la suite ne se rapproche d'aucun réels, alors elle est divergente.
Mais attention : une suite divergente admet soit une limite infinie, soit aucune limite.
On dira qu'une suite un admet pour limite +∞ si tout intervalle ouvert ]a ; +∞[ contient tous les termes de la suite un à partir d'un certain rang p. C'est-à-dire qu'à partir d'un certain nombre, que l'on désigne par a, les termes de la suite tendent vers l'infini.
Exemple
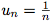tend vers 0.
En effet, cela se voit bien quand on calcule les premiers termes de la suite :
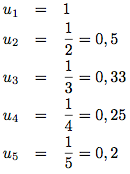
On doit calculer tous les termes de la suite pour savoir si elle converge ou pas ?
Non, pas du tout. Il faut tout de même en calculer quelques uns pour avoir une idée de la limite.
Regardez bien mon raisonnement qui peut paraître complexe la première fois.
Tout intervalle qui contient 0 contient également l'intervalle ]-a ; a[ avec a > 0, c'est de la pure logique.
Maintenant, si un ∈ ]-a ; a[, alors :
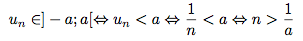
Donc, tous les termes de la suite un sont contenus dans l'intervalle ]-a ; a[ dès que n est supérieur à
.
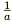Conclusion : la suite un converge vers 0.
Ne vous inquiétez pas, nous aurons des méthodes bien plus simples et plus rapides pour montrer la convergente ou la divergence d'une suite.
Et pour les suites divergentes ?
Exemple
En effet : la suite ne fais que osciller autour de 0 en prenant successivement les valeurs 1 et (-1).
Une dernière propriété, très simple en plus.
Propriété
Propriété sur la convergence
Une suite un converge vers L revient à dire que la suite (un - L) converge vers 0.Remarque