Continuité

Cours terminale ES

Nous commencerons par la continuité. C'est quelque chose de très important en mathématiques, surtout si vous voulez continuer dans cette science après le bac.

Définition

Continuité

Soit f une fonction définie sur un intervalle I et a un élément de cet intervalle I.
On dit que f est continue en un point a si :

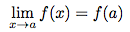
Je suppose que cette définition est un peu obscure pour vous. Je vais vous la traduire.
On prend tout d'abord une fonction f sur un intervalle I donné.
Si, quand on trace la fonction, on ne lève pas le crayon, la fonction est continu.
Si à un moment, à un point a par exemple, la fonction se "coupe", alors elle n'est pas continue.

Exemple

La fonction carrée f(x) = x² est continue sur .

Théorème

Exemple

La fonction f(x) = 2x² + 3 x - 4 est continue sur .

En effet : La fonction f est la somme de la fonction carré f(x) = x² que l'on multiplie par 2 et de la fonction f(x) = x multiplié par 3, ainsi que de la fonction constante f(x) = -4.
Or, ces trois fonctions sont continues sur .
Donc la fonction f(x) = 2x² + 3x - 4 est continue sur .

Voici un des grands théorèmes de Terminale. C'est absolument sûr que vous aurez une question en rapport à l'épreuve de Juin prochain.

Théorème

Théorème des valeurs intermédiaires

Soit f une fonction continue et strictement monotone sur [a, b].
Pour tout réel k compris entre f(a) et f(b), l'équation f(x) = k admet une unique solution dans [a, b].

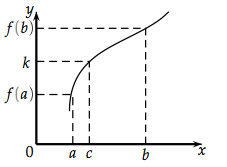
Attention, il faut absolument une fonction continue et strictement monotone sur un intervalle [a, b]. Qu'es-ce que cela veut dire ? Cela veut dire que la fonction est soit strictement croissante, soit strictement décroissante sur [a, b] et que sur cet intervalle, on peut tracer la fonction f sans levé le crayon.
Dans ces conditions là, pour tous les réel k compris dans l'intervalle [f(a), f(b)], image de l'intervalle [a, b], alors ce k admet un unique antécédent. La fonction passe obligatoirement une fois et une seule fois par ce k.

Regarder bien la figure précédente.
On a pris un intervalle [a, b] et l'intervalle [f(a), f(b)] qui n'est rien d'autre que l'image de l'intervalle [a, b].
La fonction représentée est continue et strictement monotone, en l'occurrence croissante ici.
On voit très bien que n'importe quel k compris entre f(a) et f(b) admet un antécédent par la fonction f. Vous n'avez qu'à essayer. Prenez un autre k dans l'intervalle [f(a), f(b)]. Il aura toujours un et un seul antécédent par f.

Je vais vous donner une exemple important. C'est exactement ce qu'on vous demandera de faire le jour J.

Exemple

Soit f la fonction continue définie sur [-3; 7].
On donne le tableau de variation de la fonction f ci-dessous.



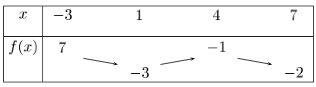
Combien de solution admet l'équation f(x) = 0 ?

• Premièrement, f est continue sur [-3; 7], comme ça on l'a dit.


• On cherche f(x)=0, donc on va chercher dans la ligne du bas du tableau de variation.

Or, 0 ∈ [-3; 7] (attention à l'ordre des nombres dans un intervalle, le plus petit d'abord). Cela correspond à l'intervalle de x [-3; 1].

• La fonction f est strictement décroissante sur [-3, 1].
• On a toutes les condition. Appliquons le théorème des valeurs intermédiaires : L'équation f(x) = 0 admet une unique solution sur l'intervalle [-3; 1].
  Mais la question est posée sur l'intervalle [-3; 7]. Il faut donc vérifié si l'équation admet une autre solution dans l'intervalle restant, soit [1; 7].
  Regardons. Non, f(x) ne passe plus par 0. En effet, elle part de -3 jusque -1, puis de -1 à -2. Donc sans passé par 0.


• Conclusion : L'équation f(x) = 0 admet une uniquement solution sur [-3; 7].