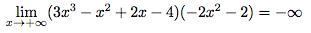Il y a une méthode pour déterminer la limite d'une fraction rationnelle polynomiale au voisinage de l'infini. C'est dans ce cours de maths que vous aller l'apprendre.
Quand on a affaire avec des fonctions polynômes, l'étude de limite en l'infini est très simplifiée grâce à ce théorème.
Propriétés
Fraction rationnelle polynomiale au voisinage de l'infini
Soit P un polynôme.- La limite de ce polynôme P en +∞ ou -∞ est égale à la limite de son terme de plus haut degré.
- La limite d'une fonction rationnelle dont le numérateur et le dénominateur sont des fonction polynômes en +∞ ou -∞ est égale à la limite du quotient des termes de plus haut degré.
Remarque importante
Attention, je précise bien, ces propriétés ne sont valables que qui on étudie la limite en +∞ ou -∞.
Exemple 1
Soit le polynôme P(x) = -x5 + 3x4 + x³ - 5x + 2.
Sa limite en +∞ est celle de son terme de plus haut degré, c'est-à-dire c'est la limite de -x5 et :
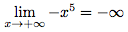
Donc, la limite de P en +∞ est -∞.
Sa limite en +∞ est celle de son terme de plus haut degré, c'est-à-dire c'est la limite de -x5 et :
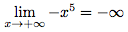
Donc, la limite de P en +∞ est -∞.
Exemple 2
On demande de calculer la limite en +∞ de 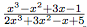 .
.
Facile. On prend les termes de plus haut degré du haut et du bas :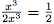 .
.
Donc :
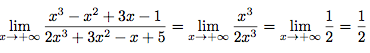
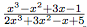 .
.
Facile. On prend les termes de plus haut degré du haut et du bas :
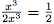 .
.
Donc :
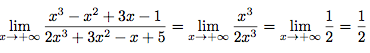
Exemple 3
Calculer la limite en +∞ de (3x³ - x² + 2x - 4)(-2x² - 2).
Or,
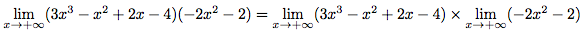
Calculons donc séparément les deux limites puis nous effectuerons leur produit.
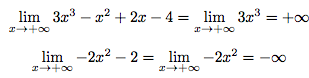
Le produit de +∞ et de -∞ est -∞.
Conclusion :
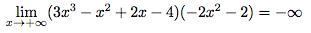
Or,
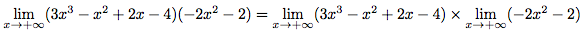
Calculons donc séparément les deux limites puis nous effectuerons leur produit.
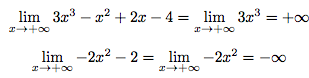
Le produit de +∞ et de -∞ est -∞.
Conclusion :