Sachez qu'il existe d'autres moyens de déterminer la limite d'une fonction. Parmi eux, le théorème de l'encadrement de fonctions. C'est en effet un moyen assez simple pour encadrer une fonction et ensuite en déduire sa limite.
Encore un théorème sur les limites de fonctions à connaître.
Théorème
Théorème de l'encadrement de fonctions et limites
Soient b un réel, u et v deux fonctions telles que :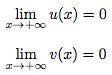
Si, pour tout x ∈ ]b, +∞[, u(x) ≤ f(x) - L ≤ v(x), alors :
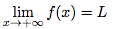
Si on arrive à encadrer la différence d'une fonction f et d'un nombre L par deux fonction qui tendent vers 0 quand x tend vers +∞, alors la limite en +∞ de la fonction f est ce nombre L.
Pour gagner du temps, je ne vous donne pas d'exemple précis d'application de ce théorème. Mais aillez-le en tête.




