On considère la fonction f définie sur R par : f(x) = x³ - 4x² + 4x.
-
Calculer la dérivée de f.
f '(x) = 3x2 - 8x + 4 -
Etudier le signe de cette dérivée.
Calculons, à l'aide de Δ, les racines de ce polynôme dérivé.
Δ = 64 - 4 × 3 × 4 = 16
D'où les racines suivantes :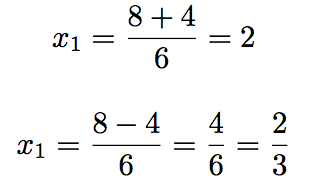
Voici donc le tableau de signes.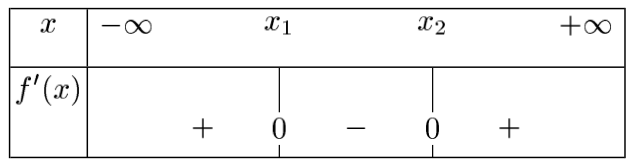
-
En déduire le tableau de variation de la fonction f.
Là où la dérivée est positive, la fonction est croissante, et là où elle est négative, la fonction est décroissante.
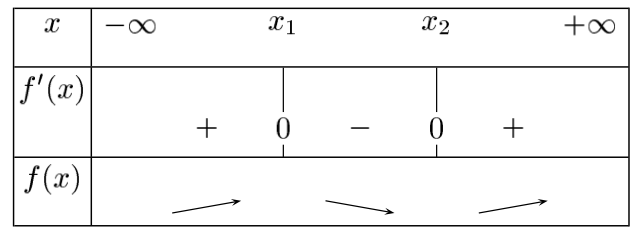
-
Tracer la courbe représentative de la fonction f dans l'intervalle [-1, 3].
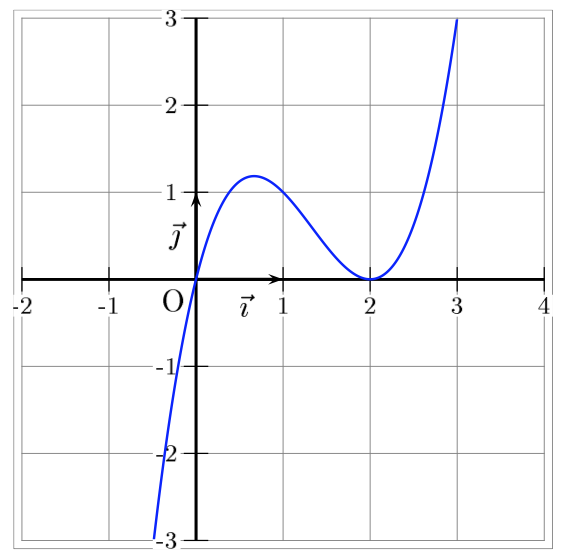
-
Déterminer par calcul les coordonnées des points d'intersection de cette courbe avec l'axe des abscisses.
Les points d'intersection de la fonction avec l'axe des abscisses sont tout simplement les points où la fonction s'annule.
On le voit aisément sur le graphique (0 et 2), mais on nous demande par calcul, donc calculons.
f(x) = 0 ⇔ x3 - 4x2 + 4x = 0 ⇔ x(x2 - 4x + 4) = 0 ⇔ x(x - 2)2 = 0
Les solutions de cette équation sont : x = 0 ou x = 2.
En remplaçant dans la fonction, on trouve que l'ordonnée des ces deux points est nulle.



