Dans chacun des cas suivants, déterminer si l'équation cartésienne de la droite en question.
-
La droite D passant par A(2; 1) et B(-1; 0).
L'équation de la droite D s'écrit : y = ax + b. On va donc chercher à trouver a et b.
On a donc le système suivant :
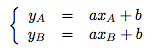
Soit :
1 = 2a + b
0 = -a + b
Que l'on résout aisément, en soustrayant la deuxième équation à la première pour trouver :
a = 1 3
En remplaçant dans l'une des deux équation précédente, on trouve facilement b :
b = 1 3
Donc, l'équation de la droite (AB) est la suivante :
y = x + 1 3 -
La droite D passant par A(-3; 0), de vecteur directeur
(1; 3).L'équation de la droite D s'écrit : ax + by + c = 0. On va donc chercher à trouver a, b et c.
Par définition, le vecteur directeur a pour coordonnées (-b; a).
Donc :
b = -1
a = 3
Il nous reste à déterminer c. Pour ce faire, nous allons utiliser justement les coordonnées du point A. On les remplace dans l'équation trouvée en remplaçant a et b par leur valeur (celles trouvées à l'instant).
3xA - yA + c = 0
3 × (-3) - 0 + c = 0
-9 + c = 0
c = 9
Donc, l'équation de la droite D est :
3x - y + 9 = 0 -
La droite D passant par A(6; -2), parallèles à la droite D' : x + y + 1 = 0
L'équation de la droite D s'écrit : ax + by + c = 0. On va donc chercher à trouver a, b et c.
Un vecteur directeur de D est(-b; a) par définition.
Or, D est parallèles à D'.
Donc, un vecteur directeur de D' est aussi un vecteur directeur de D.
Comme D' : x + y + 1 = 0, un vecteur directeur de D', et donc de D (on vient de le dire), est :
(-1; 1)
On obtient donc l'équation D de la forme :
x + y + c = 0
Il nous reste à déterminer c. Pour ce faire, nous allons utiliser justement les coordonnées du point A. On les remplace dans l'équation trouvée en remplaçant a et b par leur valeur (celles trouvées à l'instant).
xA + yA + c = 0
6 - 2 + c = 0
4 + c = 0
c = -4
Donc, l'équation de la droite D est :
x + y - 4 = 0