Dans chacun des cas suivants, déterminer si les vecteurs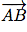 
et 
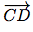sont colinéaires.
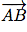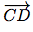et sont colinéaires.
-
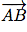(3, 5) et 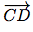(2; -6).
On a les coordonnées de deux vecteurs, il suffit d'appliquer la formule du cours pour déterminer si ces deux vecteurs sont colinéaires.
xy' - yx' = 3 × (-6) - 2 × 5 = -18 - 10 = -28 ≠ 0
Donc, les vecteurs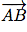 et 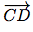ne sont pas colinéaires.
-
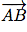(-2, 1) et 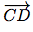(2; -1).
On a les coordonnées de deux vecteurs, il suffit d'appliquer la formule du cours pour déterminer la colinéarité de ces deux vecteurs.
xy' - yx' = (-2) × (-1) - 2 × 1 = 2 - 2 = 0
Donc, les vecteurs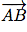 et 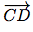sont colinéaires.
-
A(2; 4), B(3; 2), C(1; -1) et D(-3; 3).
Calculons tout d'abord les coordonnées des vecteurs
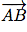et .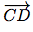
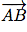(3 - 2; 2 - 4) = 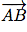(1; -2)
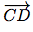(-3 - 1; 3 - (-1)) = 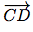(-4; 4)
Appliquons maintenant la formule du cours et c'est gagné.
xy' - yx' = 1 × 4 - (-4) × (-2) = 4 - 8 = -4 ≠ 0
Donc, les vecteurs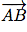 et 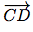ne sont pas colinéaires.
-
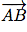(-1, 4) et 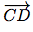(3; -12).
On a les coordonnées de deux vecteurs, appliquons la formule encore une fois.
xy' - yx' = (-1) × (-12) - 3 × 4 = 12 - 12 = 0
Donc, les vecteurs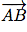 et 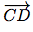sont colinéaires.
|
Fredderrty • il y a 2442 jours. J'ai aimer la resolution elle est breve.
|