Voici une partie sur le cône de révolution dans laquelle je vais vous énoncer la définition, sa formule de volume et celle de son aire latérale et enfin je terminerai par sa section plane.
Définition du cône de révolution
Nous commencerons d'abord par la définition du cône de révolution (pour changer).
Définition
Cône de révolution
Un cône de révolution est constitué d'une base en forme de disque et d'une surface conique.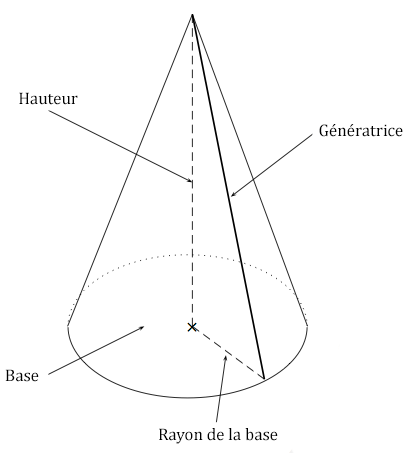
On appelle hauteur du cône de révolution, le segment perpendiculaire à la base issu du sommet.
Le rayon d'un cône de révolution est le rayon de la base.
On peut générer le cône en faisant tourner un triangle rectangle autour de la hauteur. L'hypoténuse d'un tel triangle est appelé une génératrice.
Volume du cône de révolution
Puis son volume (pour changer encore).
Propriété
Volume du cône de révolution
Le volume d'un cône de révolution s'obtient en multipliant l'aire d'une base par la hauteur, le tout divisé par 3 :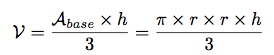
Rappelez-vous de la formule de l'aire d'un disque :
Il suffit ensuite de la multiplier par la hauteur du cône de révolution et divisé le tout par 3.
C'est en fait l'aire d'un cylindre de révolution divisé apr 3.
Exemple
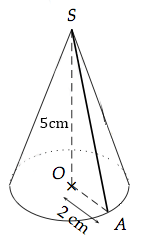
L'aire de la base, qui est un disque de rayon 2cm, vaut :
La hauteur vaut, quant à elle :
Donc, le volume de ce cône de révolution droit vaut :
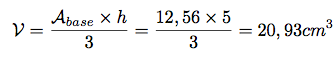
Aire latérale du cône de révolution
Je vous donne la formule pour calculer l'aire latérale d'un cône de révolution, c'est-à-dire l'aire de la surface conique.
Propriété
Aire latérale du cône de révolution
L'aire latérale du cône de révolution de rayon r et de génératrice g vaut :Je ne vous donne pas non plus d'exemple pour l'aire latérale d'un cône de révolution, c'est une simple formule à appliquer, une fois de plus.
Section plane d'un cône de révolution
Qu'obtient-on en coupant ("section") par un plan ("plane") un cône de révolution ?
Propriété
Section plane d'un cône de révolution
La section plane d'un cône de révolution par un plan parallèle à sa base est une réduction de sa base.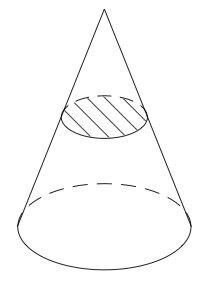
Le nouveau cône ainsi créé est une réduction du cône initial.
Cela se comprend très bien grâce à la figure. Lorsque l'on coupe un cône par un plan, on obtient un cercle plus petit que sa base.
Nous aurons l'occasion de revenir sur cette notion de réduction dans la dernière partie de ce chapitre de géométrie dans l'espace.




