Il existe plusieurs droites remarquables dans un triangle. En 5ème, nous allons en étudier trois d'entre elles : les médiatrices, les hauteurs et les médianes.
Dans un triangle, il existe des droites qui ont une signification mathématiques et qui vont nous aider à faire des calculs sur les triangles, comme par exemple calculer leur aire.
Dans ce cours, nous allons en étudier les trois principales : les médiatrices, les hauteurs et les médianes.
Médiatrice
On commence par les médiatrices. On parlera de la médiatrice d'un segment.
Définition
Médiatrice
La médiatrice d'un segment est la droite qui passe perpendiculairement en son milieu.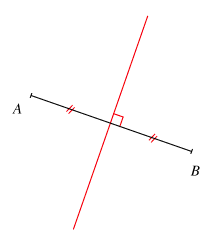
Donc, vous prenez un segment, vous tracer une droite qui passe par son milieu et qui y forme un angle droit. Cette droite est la médiatrice de ce segment.
Remarque
Propriété
Propriété des médiatrice
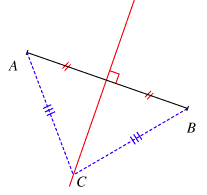
Si un point est sur la médiatrice d'un segment, il est à égale distance des extrémités de ce segment.Inversement, si un point est à égale distance des extrémités d'un segment, il appartient à la médiatrice de ce segment.
Remarque
Hauteur
Les hauteurs d'un triangle maintenant. J'en suis sûr que vous en avez déjà entendu parlé.
Définition
Hauteur
La hauteur issue d'un sommet d'un triangle est la droite qui passe par ce sommet et qui est perpendiculaire au côté opposé.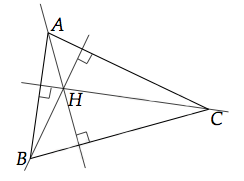
Donc, vous prenez un côté d'un triangle, vous tracer une droite perpendiculaire à ce côté et passant par le sommet opposé. Cette droite est une des hauteurs du triangle. J'ai bien dis une des hauteurs du triangle car un triangle a trois côtés, donc trois hauteurs.
Remarque
Remarque importante
Médiane
Enfin les médianes d'un triangle.
Définition
Médiane
La médiane issue d'un sommet d'un triangle est la droite passant par ce sommet et par le milieu du côté opposé.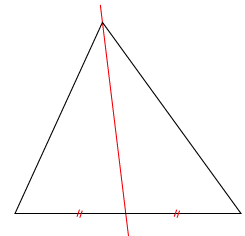
Prenez un côté d'un triangle, vous tracer une droite qui passe par le milieu de ce côté et passant par le sommet opposé. Cette droite est une des médianes du triangle. J'ai bien dis une des médianes du triangle car un triangle a trois côtés, donc trois médianes.
Remarque importante
Résumons les droites remarquables :
- Médiatrice d'un segment : Droite qui passe perpendiculairement en son milieu,
- Hauteur d'un triangle : Droite qui est perpendiculaire à un côté et qui passe par le sommet opposé,
- Médiane d'un triangle : Droite qui passe par le milieu d'un côté et par le sommet opposé.
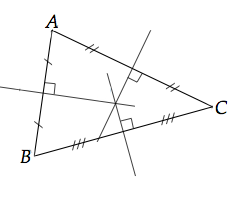
Une fois les trois construites (3 médiatrices / 3 hauteurs / 3 médianes), ces droites ont un point commun : elle se coupent en un même point chacune :
- Médiatrices d'un triangles : Centre du cercle circonscrit,
- Hauteurs d'un triangle : Orthocentre,
- Médianes d'un triangle : Centre de gravité.
Dans la partie suivante, nous allons voir plus précisément ce qu'est le cercle circonscrit à un triangle.
|
|
Ziba95 • il y a 1895 jours. Sssss |




