Un cours (qui n'est d'ailleurs plus au programme de terminale S) sur l'intégration par partie. Cette formule va vous permettre d'intégrer des fonctions un peu plus complexes.
Parfois, le calcul intégral peut s'avérer difficile.
Je vais donc vous donner un théorème très puissant pour vous sortir de toutes les mauvaises situations.
C'est la partie la plus compliquée du chapitre. Donc soyez très attentif.
Théorème
Intégration par partie
Soient u et v deux fonctions dérivables sur un intervalle I et u' et v' leurs dérivées supposées continues.Alors, pour tout réels a et b de I :
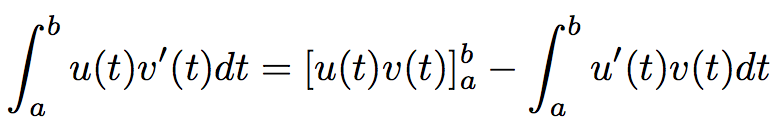
Pour bien la retenir, je vous donne la démonstration qui est à connaître.
Démonstration : On sait que (uv)'(t) = u'(t)v(t) + u(t)v'(t).
Intégrons l'égalité précédente.
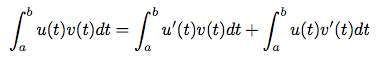
Or,
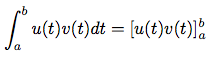
Donc :
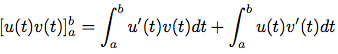
Ce qui est équivalent à :
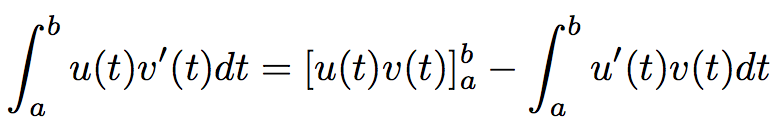
Cette formule magique va vous sortir des plus mauvaises situations.
Exemple
Calculer l'intégrale suivante :
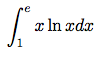
On a un produit de deux fonctions. Utilisons donc la formule d'intégration par partie.
On va donc poser u(t) et v'(t), puis déduire u'(t) et v(t).
Posons donc :
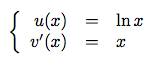
On en déduit facilement :
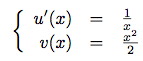
Appliquons bêtement la formule.
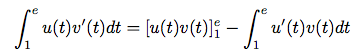
Soit :
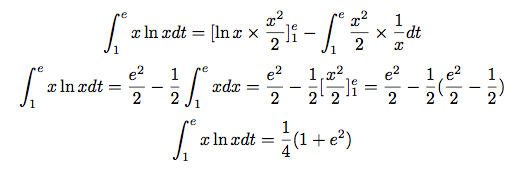
Donc, l'aire sous la courbe représentative de la fonction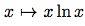
entre les droites d'équations x = 1 et x = e et l'axe des abscisses est égale à 
.
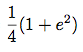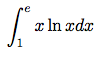
On a un produit de deux fonctions. Utilisons donc la formule d'intégration par partie.
On va donc poser u(t) et v'(t), puis déduire u'(t) et v(t).
Posons donc :
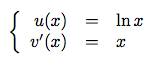
On en déduit facilement :
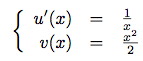
Appliquons bêtement la formule.
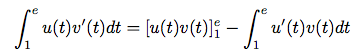
Soit :
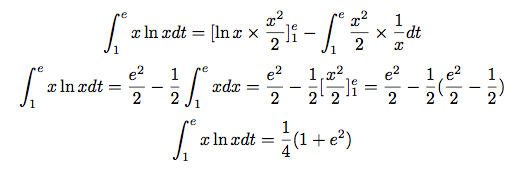
Donc, l'aire sous la courbe représentative de la fonction
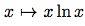entre les droites d'équations x = 1 et x = e et l'axe des abscisses est égale à .
|
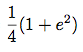Charles.clerigues • il y a 3257 jours. Lorsque l'on change de variable, il faut remplacer les x par des t car sinon il est faux de mettre dt alors qu'il y a des x dans l'intégrale |