-
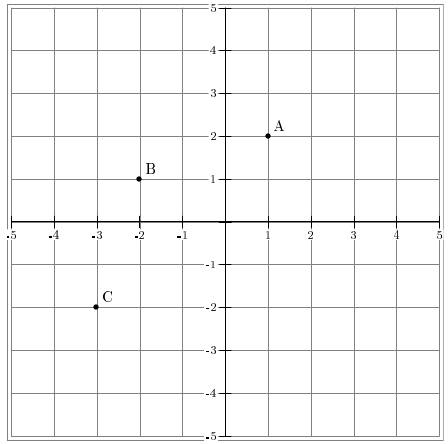
Dans ce repère, placer les points A(1;2), B(-2;1) et C(-3;-2).
Voici le repère dans lequel j'ai placé ces trois points. Rien de difficile pour le moment.
-
Calculer les distances AB et BC.
Il suffit d'appliquer la formule du cours.
Calcul de la distance AB :AB = √(xB - xA)² + (yB - yA)²
Application numérique :AB = √(-2 - 1)² + (1 - 2)² = √(-3)² + (-1)² = √9 + 1 = √10
Calcul de la distance BC :BC = √(xC - xB)² + (yC - yB)²
Application numérique :BC = √(-3 + 2)² + (-2 - 1)² = √(1)² + (-3)² = √1 + 9 = √10
Remarque : On remarque que AB = BC. Cela se voit très bien dans la figure. En effet, pour aller de A à B, on descend d'une unité et on va à gauche de 3 unités et pour aller de B à C on descend de 3 unités et on va à gauche de 1 unité. -
Calculer les coordonnées du vecteur
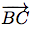 .<
.<Encore une fois, c'est une simple application de la formule.
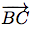 = (xC - xB; yC - yB) = (-3 - 2; -2 - 1) = (-5; -3)
= (xC - xB; yC - yB) = (-3 - 2; -2 - 1) = (-5; -3) -
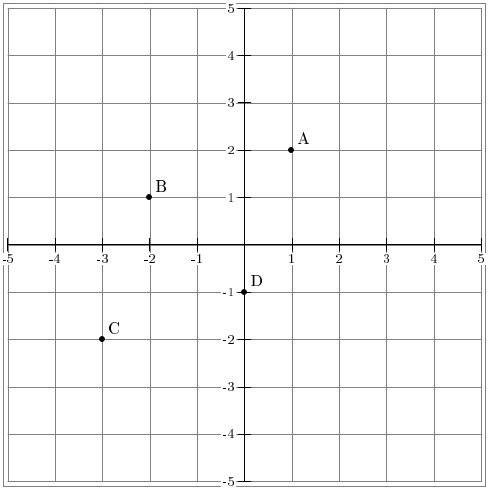
Construire le point D, image du point A par la translation qui transforme B en C.
En fait ici, il faut tout d'abord étudier la translation qui transforme B en C. En effet, comme je l'ai dit tout à l'heure, pour passer du point B au point C, on descend de 3 unités et on va à gauche de 1 unité. Eh bien là, c'est pareil, en partant de A. On descend donc de 3 unités puis 1 unité vers la gauche et on obtient le point D, image du point A par la translation qui transform B en C.
-
Démontrer que le quadrilatère ABCD est un losange.
Pour montrer qu'un quadrilatère est un losange, il faut montrer que ses quatre côtés sont égaux.
Or, on a déjà vu que AB = BC.
De plus, le point D étant l'image du point A par la translation qui transforme B en C.
Donc, forcément : AD = DC.
Calculons la distance AD pour voir si elle est égale à AB (ou BC, c'est pareil). Les coordonnées de D sont (0; -1) d'après la figure.AD = √(xD - xA)² + (yD - yA)²
Application numérique :AD = √(0 - 1)² + (-1 - 2)² = √(-1)² + (-3)² = √1 + 9 = √10
On a bien :AB = BC = AD = DC = √10
Donc, le quadrilatère ABCD est un losange.



