Soit la suite numérique un définie par :
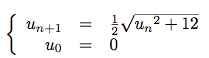
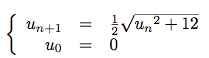
-
En calculant les premiers termes de la suite un, effectuer une conjecture sur sa limite.
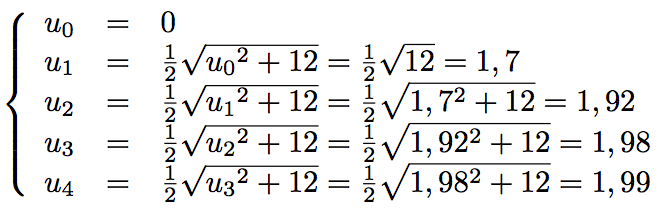
On peut conjecturer que la limite de un est 2. -
Montrer que la suite vn = un² - 4 est géométrique.
Calculons vn + 1 et essayons de trouver un q tel que : vn + 1 = qvn.
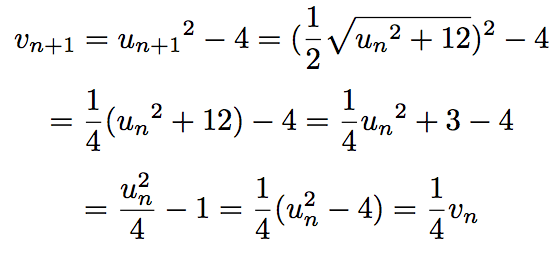
Donc, la suite vn est une suite géométrique de raison 1/4. -
Déterminer la limite de vn.
La suite vn est une suite géométrique de raison -1 < q = 1/4 < 1.
Donc, d'après le cours,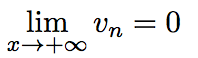
La suite vn converge vers 0. -
En déduire la limite de un.
On a :
vn = un2 - 4 ⇔ un2 = vn + 4
En faisant tout tendre vers l'infini :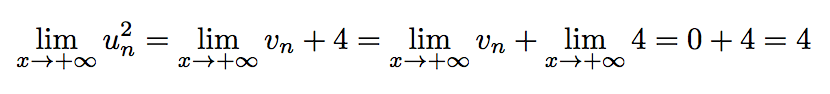
D'où :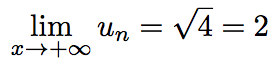
La conjecture effectuée au début de l'exercice était bonne.


